
Draw a circuit n-p-n transistor amplifier, CE configuration. Under what condition does the transistor act as an amplifier?
Answer
498k+ views
Hint: An amplifier is a device that increases the amplitude of the input signal. A transistor can act as an amplifier, the emitter base junction must be forward biased and the base collector must be reverse biased.
Formula used:
V=iR
Complete step-by-step answer:
An amplifier is a device that increases the amplitude of the input signal.
A transistor can act as an amplifier, the emitter base junction must be forward biased (FB) and the base collector must be reverse biased (RB) as shown in the figure. The load is connected between the collector and the emitter through DC supply.
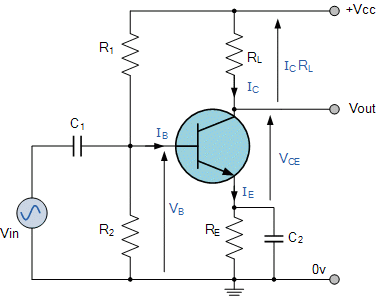
The input signal is from an AC source. The AC signal (
The output signal (amplified signal) is received between the collector and the ground (as shown).
Consider
Then by applying Kirchhoff’s loop law on the output loop we get,
Similarly,
If
When there is change in
Therefore, we can get,
Due to the change in current
Therefore,
Here,
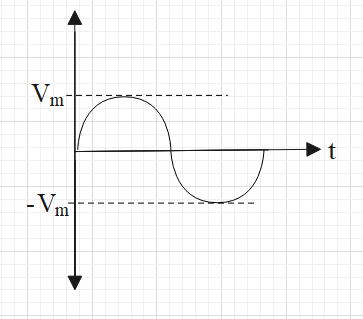
Note: Note that the output signal will be of higher amplitude than the amplitude of input signal but there will be a phase difference of pi between the two signals. Suppose the graph of input signal versus time is as follows:
Then the graph of output signal versus time will be
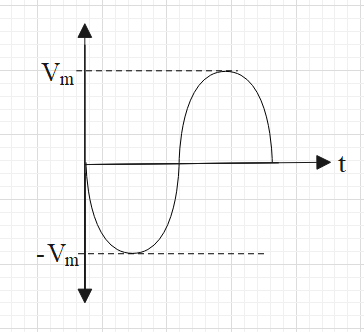
Here, you can see that the maximum voltage of the input source is being amplified. However, the phase of the amplified voltage is changed by one half cycle (i.e. angle of
Formula used:
V=iR
Complete step-by-step answer:
An amplifier is a device that increases the amplitude of the input signal.
A transistor can act as an amplifier, the emitter base junction must be forward biased (FB) and the base collector must be reverse biased (RB) as shown in the figure. The load is connected between the collector and the emitter through DC supply.

The input signal is from an AC source. The AC signal (
The output signal (amplified signal) is received between the collector and the ground (as shown).
Consider
Then by applying Kirchhoff’s loop law on the output loop we get,
Similarly,
If
When there is change in
Therefore, we can get,
Due to the change in current
Therefore,
Here,
Note: Note that the output signal will be of higher amplitude than the amplitude of input signal but there will be a phase difference of pi between the two signals. Suppose the graph of input signal versus time is as follows:

Then the graph of output signal versus time will be

Here, you can see that the maximum voltage of the input source is being amplified. However, the phase of the amplified voltage is changed by one half cycle (i.e. angle of
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE




