Question

Draw a diagram of an AC generator and describe it. Derive an expression for instantaneous value of induced emf.

Answer 1

Hint: An A.C. generator is an electronic device used to convert mechanical energy into electrical energy using the principle of electromagnetic induction. Construct the diagram by schematic analyses of its working and thus include all its essential components. The expression for induced emf can be established using the expression for magnetic flux in the coil and Faraday’s flux rule.

Formula Used:
Magnetic flux across the coil, $\phi = NBA\cos \theta $
Faraday’s flux rule, $\varepsilon = - \dfrac{{d\phi }}{{dt}}$

Complete step-by-step answer:
A generator or dynamo is a device which converts mechanical energy into electrical energy. The term generator is wrongly used to describe this device because it does not generate energy in any manner rather just converts its one form into another.
An A.C. generator is the one that produces a current that is alternating in nature or changes its direction regularly after a fixed interval of time. Thus this device converts mechanical energy into an alternating form of electrical energy.
The principle behind A.C. generators is electromagnetic induction. When a closed coil is rotated in a uniform magnetic field with its axis perpendicular to the magnetic field, the magnetic flux linked with the coil changes and an induced emf and hence current is set up in it.
The different parts of an A.C. generator include:
i. Field magnet
ii. Armature
iii. Slip rings
iv. Brushes
v. Source of energy
The following diagram shows an A.C. generator:

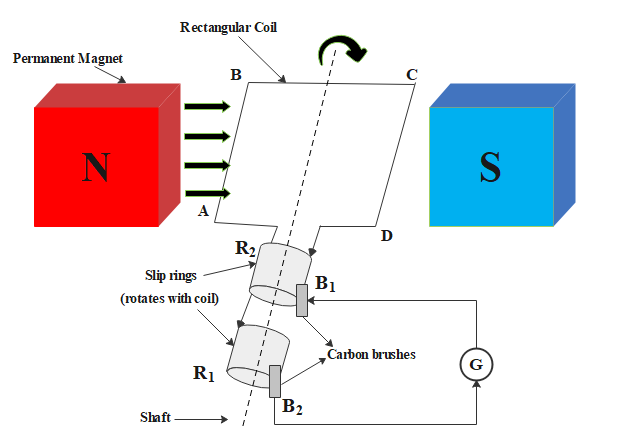
The expression for instantaneous value of induced emf:
Consider the number of turns in the coil of the A.C. generator are N, its face area for each turn is A, the magnitude of the magnetic field is B and $\theta $ is the angle which normal to the coil makes with magnetic field B at any instant t. Let the angular velocity with which the coil rotates be $\omega $.
Then the magnetic flux linked with the coil of the A.C. generator at any instant t will be given by:
$\phi = NBA\cos \theta $
or, $\phi = NBA\omega t$
By Faraday’s flux rule, the induced emf is given by:
$\eqalign{
  & \varepsilon = - \dfrac{{d\phi }}{{dt}} \cr
  & \Rightarrow \varepsilon = - \dfrac{d}{{dt}}\left( {NBA\cos \omega t} \right) \cr
  & \Rightarrow \varepsilon = NBA\omega \sin \omega t \cr
  & \therefore \varepsilon = {\varepsilon _ \circ }\sin \omega t \cr} $
where ${\varepsilon _ \circ } = NBA\omega $. This equation gives the expression for instantaneous value of induced emf.

Note: The generation of A.C. is more economical than the generation of D.C. Additionally, the alternating voltage can be easily stepped up or stepped down, as per the requirement of the circuit with the help of a transformer.