Question

Draw a labeled circuit diagram of a simple electric motor and explain its working. In what ways these simple electric motors are different from commercial motors.

Answer 1

Hint: Explain the working of the motor with a simple diagram just to understand how a motor rotates when connected to the battery. To draw the diagram just place a loop and show how the rotation effect is produced. To differentiate how commercial motors are different from simple motors consider the requirements of the motor in real life. One can also consider the modification of the simple motor to make it more effective and economical.

Complete step by step answer:
To begin with let us first draw a circuit diagram on how a motor works and what are its basic fundamentals,

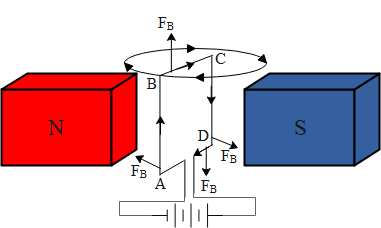
Let us consider a square loop of length a is kept in a magnetic field. The loop is connected to a battery through an axle and a constant current flows through the circuit. A current carrying wire placed in a magnetic field experience a force which is given by ${{F}_{B}}=ilB\operatorname{sin}\theta $ where i is the current in the wire, l is the length of the wire, B is the strength of the magnetic field and $\operatorname{sin}\theta =1$ is the Sine of the angle between magnetic field and the length vector is equal to 90 degrees.
The force on the length BC and AD cancels out each other hence there is no motion in the vertical direction. The force on length BA and CD are also in the opposite direction, hence the net force on the coil is zero. But the force on length BA and CD will rotate the coil producing a net torque.
This torque is equal to force on AB times the distance from the axis of rotation plus force on DC times the distance from the axis of rotation. Mathematically written as,
$\tau ={{F}_{AB}}\dfrac{a}{2}+{{F}_{DC}}\dfrac{a}{2}.....(1)$
Force due to the magnetic field is given by ${{F}_{B}}=ilB\operatorname{Sin}\theta $ In the above case sine of the angle is 1 and length of the wire is a. Therefore ${{F}_{AB}}={{F}_{DC}}=iaB$. Substituting this result in equation 1 we get,
$\tau =iaB\dfrac{a}{2}+iaB\dfrac{a}{2}$ taking iaB common we get,
$\tau =iaB\left( \dfrac{a}{2}+\dfrac{a}{2} \right)$
$\tau =i{{a}^{2}}B$ since ${{a}^{2}}$ is the area of the loop A,
$\tau =iAB$ Hence the motor will rotate with this torque.
In commercial motors the number of loops is increased as it will generate torque n times the number of loops. The loops are also coiled up as the flux through the loops increases. The magnets used in commercial motors are electromagnets which do not lose their magnetism.

Note:
Electromagnets are used in commercial motors as they use the current from the source to produce a constant magnetic field. This is required because the magnets lose magnetism after some time depending on the coercive factor. Hence the motor will stop working time after time due to the magnets which commercially are not economical.