Question

Draw a labeled diagram of an ac generator. Obtain the expression for the emf induced in the rotating coil of N turns each of cross-sectional area A, in the presence of a magnetic field $\overrightarrow B $.

Answer 1

Hint: In this question, we will learn about an ac generator through the definition and the diagram of an ac generator and the concept behind it. Then we will obtain an expression for the emf induced in the rotating coil in the presence of magnetic field. And by this knowledge and applying the formula required, we will be approaching our answer.

Step-By-Step answer:
Diagram-

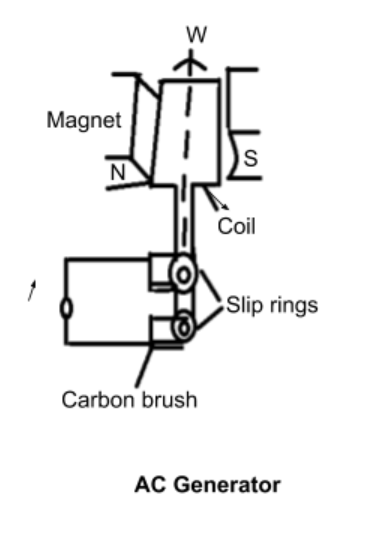
According to Faraday’s law of electromagnetic induction a machine that converts available or given energy into electrical energy is known as a generator.
They are of two types AC Generator and DC Generator. In an ac generator loss are generally lower than the dc generator and there is a difference of size too in both generators i.e. the dc generator’s size is relatively bigger than the ac generators. In an ac generator because of the step-up feature the transmission link size is thinner.
Let us take t = 0 at instant. In the direction of the magnetic field the plain of a coil is perpendicular to the direction of magnetic field i.e. coil points area of vector in the same direction as that of magnetic field the plain of the coil is perpendicular on it coil points in the same direction of the magnetic field. Hence, the flux passing through the coil is maximum.
The coil through flux is passed at t = 0,
The rotation of coil on an axis in which angular velocity is constant i.e. $\omega $ as shown in the figure.
The coil rotated on an angle in time t it wt.
Rate of change of flux $
  \dfrac{{d\theta }}{{dt}} = NBA\dfrac{d}{{dt}}(\cos \omega t) \\
  \therefore \dfrac{{d\theta }}{{dt}} = NBA \times ( - \omega \sin \omega t) \\
    \\
$
We get $\dfrac{{d\theta }}{{dt}} = - NBA\omega \sin \omega t$
Induced emf in the coil $E = \dfrac{{ - d\phi }}{{dt}}$

NOTE: Through the transformers ac generators can be stepped up and stepped down easily. AC generators which are of large power can be extremely hazardous. The basic difference between an ac and a dc generator is of their size, i.e. dc generator (current flowing in single direction) is much heavier and bigger than an ac generator (current flow based on the magnet’s movement). Hence the working.