
Draw a plot showing the variation of (i) electric field (E) and (ii) electric potential (V) with the distance r for a point charge Q.
Answer
570.9k+ views
Hint: When a point charge particle is placed at a point, it creates a force field around it. This is called the electric field (E). Now, when you move a point unit charge under this field from infinity to a particular point, the work done by the particle is called electric potential. Electric potential difference between two points is equal to work done by the unit charge point particle moving one point to another.
Complete step by step answer:
A point particle with charge Q placed at origin. From Coulomb’s law, the electric field of the charge will be,\[=\dfrac{Q}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}\widehat{r}\], assuming that it is placed in free space and \[{{\varepsilon }_{0}}\] is electric permittivity of free space. It is acting in the positive direction of r.
Now, according to definition above, the electric potential will be, \[V(r)=-\int\limits_{\infty }^{r}{}\cdot d\]. Now, putting the form of electric field and integrating over dr, we get that, \[V(r)=-\dfrac{Q}{4\pi {{\varepsilon }_{0}}r}\].
Now, plotting these two functions with respect to r, we get
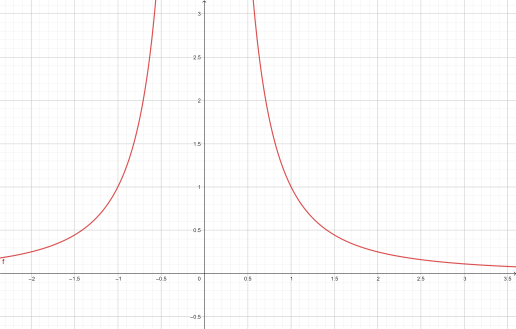
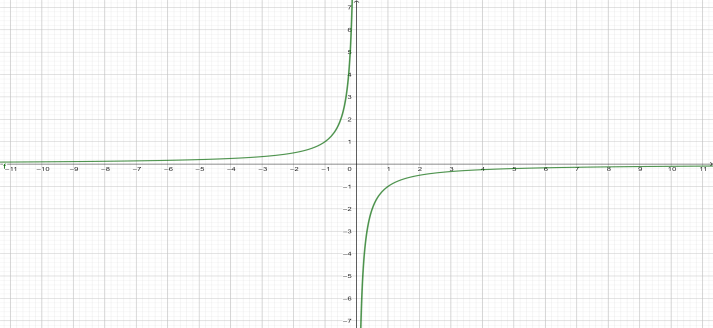
Fig-1: Electric field Fig-2: Electric potential
If we closely look at it we will see, in both cases if we take r close to origin value of potential and field goes very high. And we are ignoring the negative section of the plot, since in polar coordinates only positive values of r exist.
Note:
The S.I unit of the electric field is Newton/coulomb (N/C) which is the same as volt/meter (V/m). The S.I unit of electric potential is volt (V). In a cgs unit or Gaussian unit, the unit of electric field and electric potential is stat volt/stat coulomb and stat volt.
Complete step by step answer:
A point particle with charge Q placed at origin. From Coulomb’s law, the electric field of the charge will be,\[=\dfrac{Q}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}\widehat{r}\], assuming that it is placed in free space and \[{{\varepsilon }_{0}}\] is electric permittivity of free space. It is acting in the positive direction of r.
Now, according to definition above, the electric potential will be, \[V(r)=-\int\limits_{\infty }^{r}{}\cdot d\]. Now, putting the form of electric field and integrating over dr, we get that, \[V(r)=-\dfrac{Q}{4\pi {{\varepsilon }_{0}}r}\].
Now, plotting these two functions with respect to r, we get


Fig-1: Electric field Fig-2: Electric potential
If we closely look at it we will see, in both cases if we take r close to origin value of potential and field goes very high. And we are ignoring the negative section of the plot, since in polar coordinates only positive values of r exist.
Note:
The S.I unit of the electric field is Newton/coulomb (N/C) which is the same as volt/meter (V/m). The S.I unit of electric potential is volt (V). In a cgs unit or Gaussian unit, the unit of electric field and electric potential is stat volt/stat coulomb and stat volt.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Differentiate between action potential and resting class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




