Question

Draw a tetrahedron in isometric dot paper.

Answer 1

Hint: We first take two dots A,B on the isometric graph paper and join AB. We take a dot above AB as C and then join AC and BC. We take a dot D inside the triangle ABC and then join AD,BD,CD. We have the required tetrahedron ABCD.

Complete step by step answer:
A tetrahedron otherwise known as a triangular pyramid is a polyhedron composed of four triangular faces , four vertex corners and six edges joining those four vertex corners.
Isometric graph paper is a type of graph paper with the all points or the dots having equidistant from the nearest points. Isometric Graph Paper unlike regular graph paper does not have grids.
We take two isometric dots on a horizontal line with a minimum 3 unit distance. We name them A and B. These two points will be the vertices of the tetrahedron. We joined AB. The line segment AB will act at the edge of the tetrahedron.

We then take an isometric dot as a point denoted as C above or below (we have taken here above) and join BC and AC. We obtained another vertex C and two other edges BC and AC of the tetrahedron.

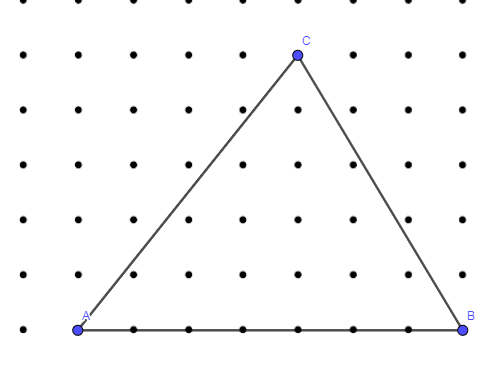
We have now obtained a triangle ABC which will act as a triangular face of the required tetrahedron. We take an isometric dot in the interior of the triangle ABC. We denote this dot as D. D is the fourth and final vertex of the tetrahedron. We then joined AD, BD, CD.

We have obtained the tetrahedron ABCD with vertex at the top C and the triangular base at the bottom is ABD. The six edges are AB, AC, AD, BC, BD and CD. The triangular faces are ABC, ABD, ACD, CBD.

Note: We can also draw regular tetrahedron whose lengths of the edges are equal. In that case we have to locate the point C at the perpendicular bisector of AB such that AB=BC=AC. Then we locate D such that CD=AD=BD=AB. A shape or an object is drawn in isometric graph paper using isometric projections. We used the orthogonal projection on the edges not on the vertices to draw the tetrahedron here.