Question

Draw a velocity time graph for an object in uniform motion. Show that the area under the velocity-time graph gives the displacement of the object in the given time interval.

Answer 1

Hint: For a body in uniform motion, the magnitude of its velocity remains constant over time, that is, it has zero tangential acceleration that can change its speed. Hence, for uniform motion, the velocity-time graph will be a straight line.

Formula used:
$\text{velocity = }\dfrac{\text{Displacement}}{\text{time}}$
$\therefore \text{Displacement = Velocity}\times \text{time}$

Complete step-by-step answer:
In uniform motion, the speed of the body remains constant, that is, the magnitude of the velocity does not change as there is no tangential acceleration.
Since, acceleration is the slope of the velocity-time graph, if it is zero, then the slope will also be zero. Therefore, the graph will be nothing but a straight horizontal line with zero slope.
Therefore, let us now draw the graph.

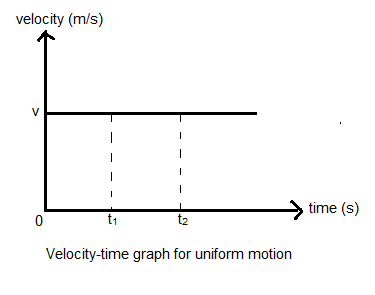
To show that the area under the velocity time graph gives the displacement of the body, we will find out the area of the rectangle between the dotted lines as shown in the graph.
Since, the area of the rectangle is nothing but its $\text{length}\times \text{breadth}$, we will get the area of the rectangle as $v\times \left( {{t}_{2}}-{{t}_{1}} \right)$ --(1)
Where $v$ is the constant magnitude of velocity of the body and $\left( {{t}_{2}}-{{t}_{1}} \right)$ is the span of the time interval.
Now, $\text{velocity = }\dfrac{\text{Displacement}}{\text{time}}$ $\therefore \text{Displacement = Velocity}\times \text{time}$ --(2)
Hence, comparing (1) and (2), we get,
The area under the rectangle is nothing but the displacement covered by the body in that time interval.

Note: Students must be aware that uniform velocity and uniform motion are different. In uniform motion, the speed of the body remains constant, however its direction does not. Therefore, tangential acceleration has to be zero, but radial acceleration may not. On the other hand, since velocity is a vector it has both direction and magnitude. So, in uniform velocity, both the magnitude and direction of the velocity remain constant. Thus both radial and tangential acceleration have to be zero. Therefore a body going around a circle at constant speed also executes uniform motion but does not have uniform velocity.