Question

Draw an isosceles triangle ABC in which $\text{AB = AC = 6}$ cm and $BC\text{ }=\text{ }5$cm. Construct a triangle PQR similar to $\Delta ABC$ in which PQ = 8 cm. Justify the construction. \[\]

Answer 1

Hint: First draw the isosceles triangle ABC. Then take the point B=Q as the vertex of the triangle PQR. Then use the similarity condition given in the question to draw BR to BC with respect to the ratio of sides. And PR parallel to AC.\[\]

Complete step by step answer:
Let us first construct $\Delta ABC$ step wise.\[\]
1. We draw a line segment BC=5cm using compass and ruler.\[\]

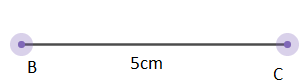
2. We draw its perpendicular bisector by taking an arc of 6cm at B and C. Then we join the points of intersection OQ.\[\]

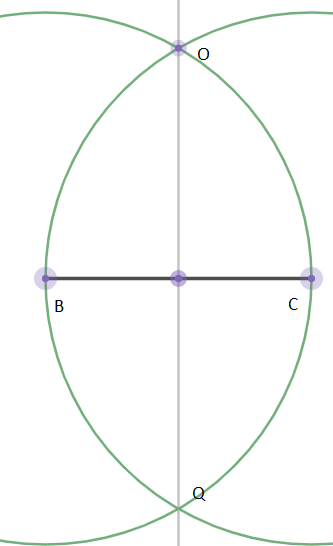
3. We draw an arc of 6cm and the point of intersection of the arc and OQ is A. \[\]

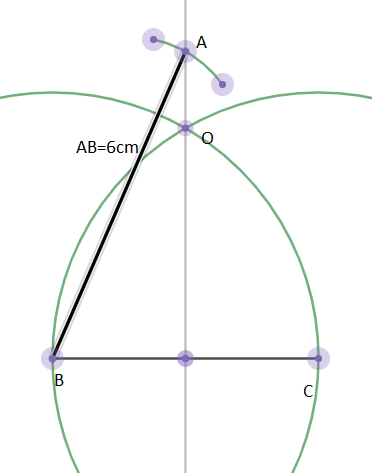
4. We join AC and the isosceles triangle ABC is obtained.

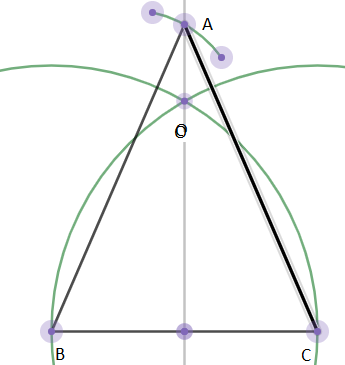
Justification: The point A will lie on the bisector because it is point to common to the equal sides AB and AC in the given isosceles triangle. \[\]
Now we shall construct $\Delta PQR$ stepwise.\[\]
1. We draw any ray BX which makes an acute angle $\angle CBX$ under BC. \[\]

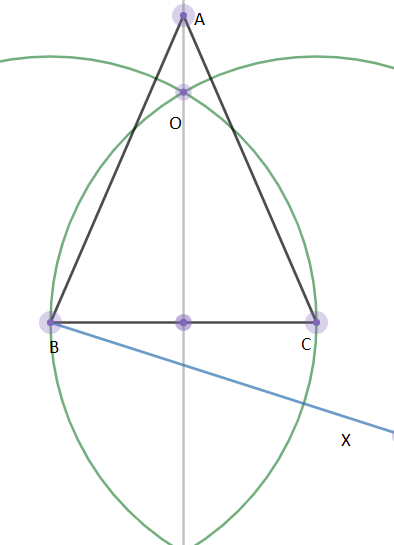
2. We locate four points ${{B}_{1}},{{B}_{2}},{{B}_{3}},{{B}_{4}}$ such that $B{{B}_{1}}={{B}_{1}}{{B}_{2}}={{B}_{2}}{{B}_{3}}={{B}_{3}}{{B}_{4}}$ by arc of equal length using the compass. \[\]

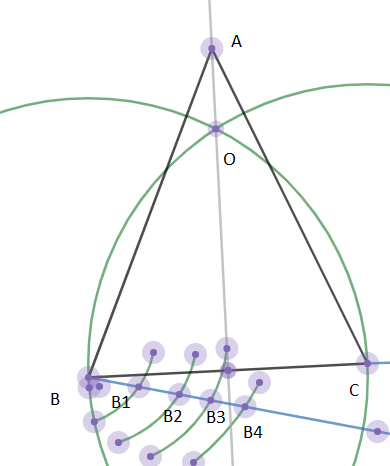
3. We join ${{B}_{3}}C$ and draw a line ${{B}_{4}}R$ where such that ${{B}_{3}}C||{{B}_{4}}R$ by taking arc of length${{B}_{3}}C$ and the arc of angle $\angle B{{B}_{3}}C$. Here R is the point of intersection of BC extended and the parallel line drawn from ${{B}_{4}}$\[\]

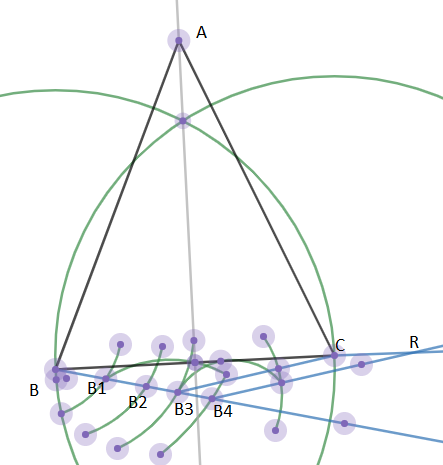
4. Similarly draw $RP||CA$ from copying the arc of length CA and the measure of angle $\angle ACB$ where P is point of intersection of the parallel line draw from R and extended line BA. \[\]

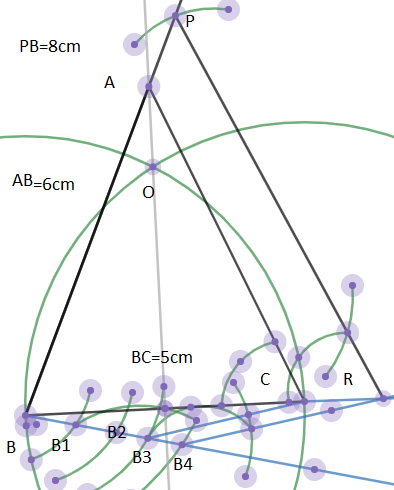
5. Now we can verify that$PB=8cm$. If we rename B as Q we get our required triangle PQR.\[\]
Justification:\[\]
It is given that the two triangles are similar which means the sides will be in ratio. We here have taken the ratio $PQ:PA=8:4=4:3$. Now our goal is to make BR=QR and CR $\dfrac{4}{3}$ times of BC and AC . Suppose from the construction $B{{B}_{1}}={{B}_{1}}{{B}_{2}}={{B}_{2}}{{B}_{3}}={{B}_{3}}{{B}_{4}}=x$
\[\begin{align}
  & BC=3x \\
 & CR=x \\
 & \dfrac{CR}{BC}=\dfrac{1}{3} \\
 & \therefore \dfrac{BR}{BC}=\dfrac{BC+CR}{BC}=1+\dfrac{CR}{BC}=1+\dfrac{1}{3}=\dfrac{4}{3} \\
\end{align}\]
We then have drawn $RP||CA$ and using Angle-angle-angle $\left( \because \angle PBC=\angle ABC,\angle ACB=\angle PRB \right)$ similarity we get $\Delta PBR\sim \Delta ABC$. So $\dfrac{PR}{CA}=\dfrac{4}{3}$.\[\]

Note: The most important assumption here we have taken here is B=Q that means both the triangles have a common vertex. We can also take the point C as the common vertex . We can verify the construction using a ruler to measure PR and QR. .