
Draw an ogive for the following data which gives the marks and numbers of students:
Marks Students
| Marks | |||||
| Students |
Answer
489.9k+ views
Hint: To, draw an ogive of the given data set, we will have to find the cumulative frequency at each interval. After that we can plot a graph of marks vs cumulative frequency. Here, as it is not mentioned whether to draw a “less than” ogive or a “more than” ogive, we can draw a simple “less than” ogive where the cumulative frequency increases with each class considered.
Complete step-by-step answer:
As we will have to find out cumulative frequency at each class, and then plot a graph using the values of cumulative frequency and marks, it is best to draw a table with three columns as class interval, frequency and cumulative frequency.
Now, as we have the values of cumulative frequency at each interval, we can plot a graph between the upper limit of each interval and the cumulative frequency at that class. Remember, the reason why we are plotting the graph with upper limit of the interval is because we are drawing a “less than” type ogive where the cumulative frequency at an interval is less than the upper limit of that interval.
The graph plotted between upper limit of interval and cumulative frequency will be as follows.
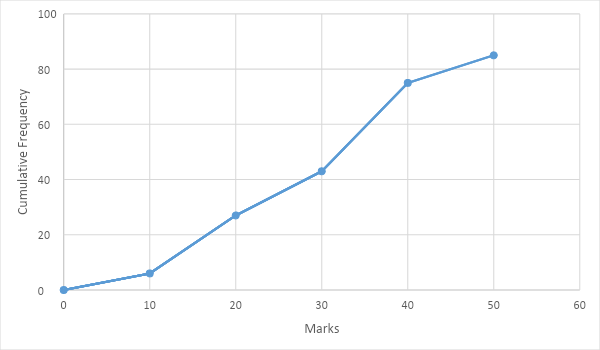
This will be the ogive for the given set of data.
Note: If we want to find the median for the data, we can do it by finding the value of x-coordinate when the value of cumulative frequency is half of maximum. By observing the graph, we can easily say that when the cumulative frequency is
Complete step-by-step answer:
As we will have to find out cumulative frequency at each class, and then plot a graph using the values of cumulative frequency and marks, it is best to draw a table with three columns as class interval, frequency and cumulative frequency.
| Class interval | Frequency | Cumulative frequency |
| 6 | 6 | |
| 21 | 27 | |
| 16 | 43 | |
| 32 | 75 | |
| 10 | 85 |
Now, as we have the values of cumulative frequency at each interval, we can plot a graph between the upper limit of each interval and the cumulative frequency at that class. Remember, the reason why we are plotting the graph with upper limit of the interval is because we are drawing a “less than” type ogive where the cumulative frequency at an interval is less than the upper limit of that interval.
The graph plotted between upper limit of interval and cumulative frequency will be as follows.

This will be the ogive for the given set of data.
Note: If we want to find the median for the data, we can do it by finding the value of x-coordinate when the value of cumulative frequency is half of maximum. By observing the graph, we can easily say that when the cumulative frequency is
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is the difference between resemblance and sem class 12 social science CBSE

What is the Full Form of PVC, PET, HDPE, LDPE, PP and PS ?

Draw ray diagrams each showing i myopic eye and ii class 12 physics CBSE

Why do the transition elements have higher enthalpies class 12 chemistry CBSE

What are the advantages of parallel combination over class 12 physics CBSE

What are the causes of overloading class 12 physics CBSE




