Question

Draw boundary surface diagrams of any four orbitals of subshell.

Answer 1

Hint: We can define a boundary surface diagram that has a good diagrammatical that represents shapes of atomic orbitals. We know there are four different kinds of orbitals, represented as s, p, d and f each with a different shape. Of the four, s and p orbitals are considered because these orbitals are of most common in organic and biological chemistry. We must remember that the s-orbital is spherical in shape with the nucleus that lies at its centre, p-orbitals are dumbbell-shaped and 4 of the five d orbitals have the shape of cloverleaf. The fifth d orbital looks like an elongated dumbbell with a doughnut about its middle. The orbitals in an atom are structured into various layers or electron shells.

Complete step by step answer: Now we are going to discuss about the features of a boundary surface diagram as,
Shape of the surface diagram: The boundary surface diagram of an orbital is independent of principle quantum number.
- Nodes in the surface diagram: The region that has very low probability density that goes to zero is called as nodes. Boundary surface diagram of s-orbital contains (n-1) nodes with ‘n’ principle quantum number. This type of node is observed in the surface diagram of p, d and f orbitals.
- Size of the surface diagram: The boundary surface diagram of an orbital raise in size or volume with raise in principle quantum number (n).
For any four orbitals of subshell we can give the boundary surface diagram as follows,

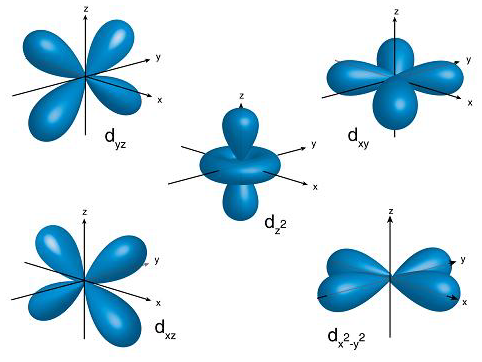
Note: We must remember that the s, p, d, and f are respectively sharp, primary, diffuse, and fundamental. We can give the magnetic orbital quantum number for d orbitals as (-2,-1, 0, 1, 2). Hence, we can say that there are five d-orbitals. These orbitals are designated as \[dxy\],\[dyz\], \[dxz\], \[{d_{{x^2}-{y^2}}}\] and \[d{z^2}\]. Out of these 5 d orbitals, shapes of the first 4 d-orbitals are similar to each other that are different from the \[d{z^2}\] orbital whereas the energy of all five d orbitals is the same.