Question

Draw five triangles and measure their sides. Check in each case, if the sum of the lengths of any two sides is always less than the third side.

Answer 1

Hint: To check that the sum of the lengths of any two sides is always less than the third, first we will draw 5 triangles of different measures of their sides. By assuming that the sum of any two sides of a triangle is greater than third sides we can prove that the sum of the lengths of any sides is not always less than the third side.

Complete step by step solution:
To prove that the sum of two sides is greater than the third side, let us draw 5 triangles with different measures of their sides and consider it as $\Delta 1,\Delta 2,\Delta 3,\Delta 4\And \Delta 5$ .
Now, we will draw $\Delta 1.$

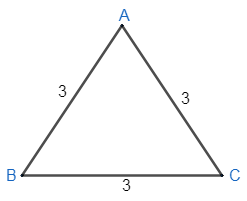
In the above $\Delta 1$ ABC,
$\begin{align}
  & AB=3; \\
 & BC=3; \\
 & AC=3. \\
\end{align}$
Let us assume that, the sum of two sides of a triangle is greater than the other side, to prove this let us take –
$\begin{align}
  & AB+BC>AC; \\
 & AB+AC>BC; \\
 & BC+AC>AB. \\
\end{align}$
By substituting the values of AB, BC & AC in each equation we get –
$\begin{align}
  & \Rightarrow AB+BC>AC \\
 & 3+3>3 \\
 & 6>3 \\
\end{align}$
$\begin{align}
  & \Rightarrow AB+AC>BC \\
 & 3+3>3 \\
 & 6>3 \\
\end{align}$
$\begin{align}
  & \Rightarrow BC+AC>AB \\
 & 3+3>3 \\
 & 6>3 \\
\end{align}$
In this case, our assumption is correct. The sum of the two sides of a triangle is greater than the third side.
Now, we will draw $\Delta 2.$

In the above $\Delta 2$ ABC,
$\begin{align}
  & AB=3; \\
 & BC=4; \\
 & AC=3. \\
\end{align}$
Let us assume that, the sum of two sides of a triangle is greater than the other side, to prove this let us take –
$\begin{align}
  & AB+BC>AC; \\
 & AB+AC>BC; \\
 & BC+AC>AB. \\
\end{align}$
By substituting the values of AB, BC & AC in each equation we get –
$\begin{align}
  & \Rightarrow AB+BC>AC \\
 & 3+4>3 \\
 & 7>3 \\
\end{align}$
$\begin{align}
  & \Rightarrow AB+AC>BC \\
 & 3+3>4 \\
 & 6>4 \\
\end{align}$
$\begin{align}
  & \Rightarrow BC+AC>AB \\
 & 4+3>3 \\
 & 7>3 \\
\end{align}$
In this case, our assumption is correct. The sum of the two sides of a triangle is greater than the third side.
Now, we will draw $\Delta 3.$

$\begin{align}
  & AB=3; \\
 & BC=2; \\
 & AC=4. \\
\end{align}$
Let us assume that, the sum of two sides of a triangle is greater than the other side, to prove this let us take –
$\begin{align}
  & AB+BC>AC; \\
 & AB+AC>BC; \\
 & BC+AC>AB. \\
\end{align}$
By substituting the values in each equation we get –
$\begin{align}
  & \Rightarrow AB+BC>AC \\
 & 3+2>4 \\
 & 5>4 \\
\end{align}$
$\begin{align}
  & \Rightarrow AB+AC>BC \\
 & 3+4>2 \\
 & 7>2 \\
\end{align}$
$\begin{align}
  & \Rightarrow BC+AC>AB \\
 & 2+4>3 \\
 & 6>3 \\
\end{align}$
In this case, our assumption is correct. The sum of the two sides of a triangle is greater than the third side.
Now, we will draw $\Delta 4.$

$\begin{align}
  & AB=5.5; \\
 & BC=6; \\
 & AC=5. \\
\end{align}$
Let us assume that, the sum of two sides of a triangle is greater than the other side, to prove this let us assume –
$\begin{align}
  & AB+BC>AC; \\
 & AB+AC>BC; \\
 & BC+AC>AB. \\
\end{align}$
By substituting the values in each equation we get –
$\begin{align}
  & \Rightarrow AB+BC>AC \\
 & 5.5+6>5 \\
 & 11.5>5 \\
\end{align}$
$\begin{align}
  & \Rightarrow AB+AC>BC \\
 & 5.5+5>6 \\
 & 10.5>6 \\
\end{align}$
$\begin{align}
  & \Rightarrow BC+AC>AB \\
 & 6+5>5.5 \\
 & 11>5.5 \\
\end{align}$
In this case, our assumption is correct. The sum of the two sides of a triangle is greater than the third side.
Now, we will draw $\Delta 5.$

$\begin{align}
  & AB=6; \\
 & BC=10; \\
 & AC=5. \\
\end{align}$
Let us assume that, the sum of two sides of a triangle is greater than the other side, to prove this let us take –
$\begin{align}
  & AB+BC>AC; \\
 & AB+AC>BC; \\
 & BC+AC>AB. \\
\end{align}$
By substituting the values in each equation we get –
$\begin{align}
  & \Rightarrow AB+BC>AC \\
 & 6+10>5 \\
 & 16>5 \\
\end{align}$
$\begin{align}
  & \Rightarrow AB+AC>BC \\
 & 6+5>10 \\
 & 11>10 \\
\end{align}$
\[\begin{align}
  & \Rightarrow BC+AC>AB \\
 & 10+5>6 \\
 & 15>6 \\
\end{align}\]
In this case, our assumption is correct. The sum of the two sides of a triangle is greater than the third side.
Hence, our assumption is correct. The sum of any two sides of a triangle is always greater than the third side but not less than the third side.

Note: Students should know that, according to triangle inequality for any given triangle. The sum of two sides of a triangle is always greater than the third side. A polygon bounded by three line-segments is known as the triangle. It is the smallest possible polygon. A triangle has three sides, three vertices, and three interior angles. The types of triangles are based on their angle measure and length of the sides. The inequality theorem is applicable for all types of triangles such as equilateral, isosceles and scalene.