
Draw logic diagram for the following Boolean expression
$Y=(\overline{\text{A}}+B)\centerdot (A+\overline{\text{B}})$. Also write it’s truth table
Answer
581.1k+ views
Hint: To draw the logic diagram of the above Boolean expression we first need to know the loci symbol for different logic operations. We also need to know how the operations function so that we accordingly give the input. Once we know the operations and the logic symbols of Boolean expressions then we can write the truth table as well as draw the logic diagram for the given Boolean expression.
Complete answer:
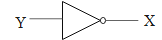
There are three basic logic gates. The first and the basic one is NOT a gate. The output due to this logic gate is nothing but the complement of the input signal. Let us say our input signal is Y than the output signal X is given by $X=\overline{Y}$. This gate is denoted by the symbol given below.
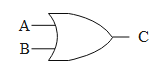
The next gate we are going to discuss is the OR gate. This gate has basically two inputs and one output. The operation performed on the two input signals is such that the output due to the gate is equal to the sum of the two input signals. Let us say the two inputs are A and B. Then the output C is given by,
$C=A+B$ .The logic symbol for the gate is given below.
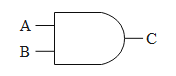
The last basic gate is the AND gate. This gate also has two inputs and one output. The operation performed on the two input signals is such that the output due to the gate is equal to the product of the two input signals. Let us say the two inputs are A and B. Then the output C is given by, $C=A\centerdot B$ .The logic symbol for the gate is given below.
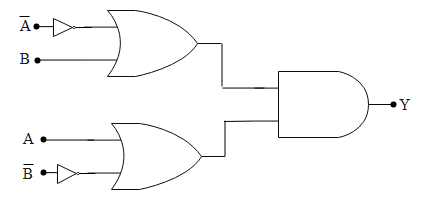
The logic gate has basically its inputs equal to either one or zero. Let us say we are constructing a logic gate for the above expression i.e. $Y=(\overline{\text{A}}+B)\centerdot (A+\overline{\text{B}})$. Let us say A and B are the two inputs and Y is the output. Let us first determine the truth table of the above Boolean equation such that we take different possibilities of inputs A and B.
Now from the symbols we know let us construct the logic gate having the input A and B and the output as Y.
Note:
To draw the logic gate of any Boolean expression we need to know how to change the input signals accordingly as per the requirements. There are two more universal logic gates. One is known as the NOR gate that is not of OR gate and the other is NAND gate which is not of AND.
Complete answer:
There are three basic logic gates. The first and the basic one is NOT a gate. The output due to this logic gate is nothing but the complement of the input signal. Let us say our input signal is Y than the output signal X is given by $X=\overline{Y}$. This gate is denoted by the symbol given below.

The next gate we are going to discuss is the OR gate. This gate has basically two inputs and one output. The operation performed on the two input signals is such that the output due to the gate is equal to the sum of the two input signals. Let us say the two inputs are A and B. Then the output C is given by,
$C=A+B$ .The logic symbol for the gate is given below.

The last basic gate is the AND gate. This gate also has two inputs and one output. The operation performed on the two input signals is such that the output due to the gate is equal to the product of the two input signals. Let us say the two inputs are A and B. Then the output C is given by, $C=A\centerdot B$ .The logic symbol for the gate is given below.

The logic gate has basically its inputs equal to either one or zero. Let us say we are constructing a logic gate for the above expression i.e. $Y=(\overline{\text{A}}+B)\centerdot (A+\overline{\text{B}})$. Let us say A and B are the two inputs and Y is the output. Let us first determine the truth table of the above Boolean equation such that we take different possibilities of inputs A and B.
| A | B | $\overline{A}$ | $\overline{B}$ | $\overline{A}+B$ | $A+\overline{B}$ | $Y=(\overline{A}+B)\centerdot (A+\overline{B})$ |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
Now from the symbols we know let us construct the logic gate having the input A and B and the output as Y.

Note:
To draw the logic gate of any Boolean expression we need to know how to change the input signals accordingly as per the requirements. There are two more universal logic gates. One is known as the NOR gate that is not of OR gate and the other is NAND gate which is not of AND.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




