
Draw phasor diagram of
Answer
449.1k+ views
Hint :In order to solve this question, we are going to first take the circuit for the
Complete Step By Step Answer:
An
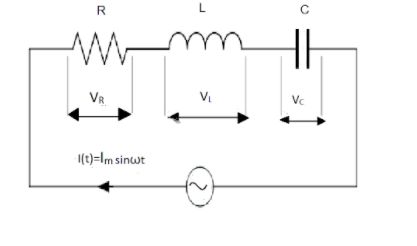
The current relation for this circuit is given by
In order to draw the phase diagram, we use the following facts:
(1) The instantaneous voltage across the pure resistance
(2) The instantaneous voltage across the pure inductance
(3) The instantaneous voltage across the pure inductance
Thus, the phasor diagram for the circuit can be drawn to depict these voltages as:
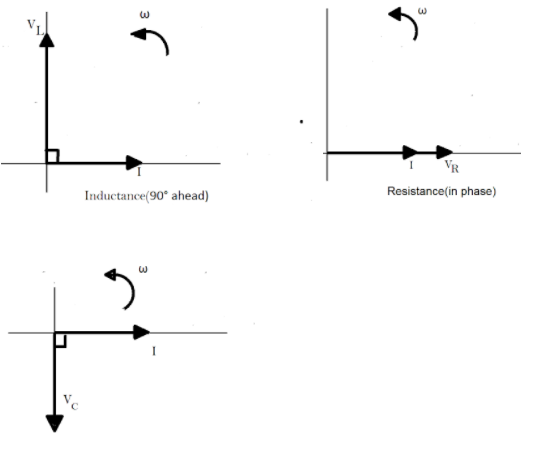
Note :
We cannot simply add the voltages
Complete Step By Step Answer:
An

The current relation for this circuit is given by
In order to draw the phase diagram, we use the following facts:
(1) The instantaneous voltage across the pure resistance
(2) The instantaneous voltage across the pure inductance
(3) The instantaneous voltage across the pure inductance
Thus, the phasor diagram for the circuit can be drawn to depict these voltages as:

Note :
We cannot simply add the voltages
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




