Question

Draw ray diagram to show the formation of three times magnified (a) real, and (b) virtual image of an object by a converging lens. Mark the position of O, F and2F in each diagram.

Answer 1

Hint: Magnification is defined as the ratio of the distance of the image to the distance of the object. Magnification is the ratio of the distance of image (v) to that of the distance of the object from the lens. Magnification can be also defined as the height of image formed to the height of the object.
Formula used:
$m = \dfrac{v}{u} = \dfrac{{{h_i}}}{{{h_o}}}$
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Where,
u=distance of object
v=distance of image
=height of the image formed
=height of object
m=magnification of lens
f=focal length of the lens

Complete step-by-step answer:
To solve this problem lets first write the given,
Magnification, m=3.
Let us use the formula for magnification,
$m = \dfrac{v}{u} = \dfrac{{{h_i}}}{{{h_o}}}$
Put the values for the magnification and equate it with respect to the distance of image formed i.e.
We get,
$3 = \dfrac{v}{u} \Rightarrow v = 3u$ ------------- (1)
1. When we placed the object in between the ‘f’ and ‘2f’;

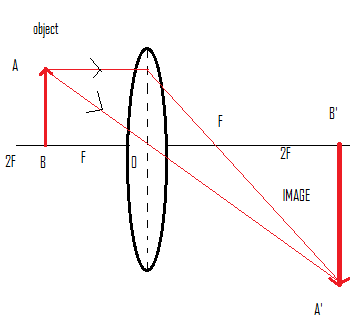
The above is the diagram of three time’s magnified real image.
Where, AB =height of object, A’B’=height of image formed
The image formed is inverted and real thus using Cartesian sign we know that,
 For real image, u= negative, v= positive (using Cartesian sign)
Now let us use the lens formula,
 $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Now let us substitute the values, we get,
$\dfrac{1}{f} = \dfrac{1}{{3u}} - \dfrac{1}{{ - u}} = \dfrac{4}{{3u}}$
Hence, focal length will be,
 $f = \dfrac{3}{4}u$
Or we can write ‘u’ in terms of f will be as,
$u = \dfrac{4}{3}f$ ------- (2)
We can draw the conclusion that is, when we placed the object in between the ‘f’ and ‘2f’, then the image formed is real, inverted and enlarged.

2. When Object is placed between focus and optical center;
 

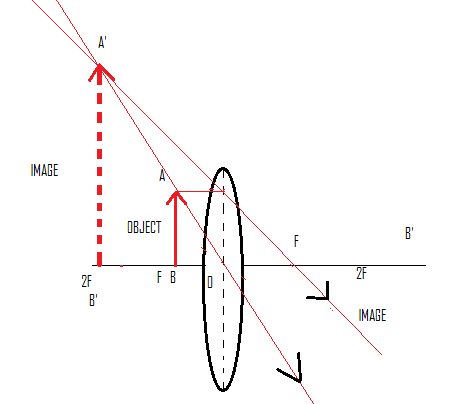
Following is the diagram of three time’s magnified virtual image.
u=negative and v=negative.
Let us use the lens formula$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$.
Let us make use of equation (1) and substitute the values in the formula.
$\dfrac{1}{f} = \dfrac{1}{{ - 3u}} - \dfrac{1}{{ - u}} = \dfrac{2}{{3u}}$
Let us write u in terms of f.
$u = \dfrac{2}{3}f$
From the diagram we can conclude that,
When we placed the object in between the focus ’f’ and optical center ’o’ ,then in such case image formed is virtual ,erect and enlarged.
Additional information:
Convex lens is known as a converging lens.
A real image is formed by the real intersection of reflected or refracted light rays. Whereas virtual image is formed by the virtual intersection of reflected or refracted light rays.
Real image formed is always inverted however the virtual image formed as erect.
A real image can be obtained on the screen whereas a virtual image cannot be obtained on the screen.
 Real image appears only when the rays converge. Virtual images appear when rays diverge.
Note:
Converging lens is convex lens and converging mirror is concave mirror.
If the object is placed away from the mirror ,then the real image is formed by concave mirrors
Magnification :
For real images: Negative (-ve)
For virtual images: Positive (+ve).