Question

Draw the graph of $sin^2x$ and $|sinx|$ and show the continuity and differentiability of both the functions.

Answer 1

Hint: To show the continuity of a function, we should ensure that it exists at all points and there are no breaks or sharp edges on the graph of that function. To check the differentiability of a function $f(x)$ at a point, the formula is-
$\lim_{\mathrm h\rightarrow0}\dfrac{\mathrm f\left(\mathrm x+\mathrm h\right)-\mathrm f\left(\mathrm x\right)}{\mathrm h}\;\mathrm{exists}\;\mathrm{at}\;\mathrm{all}\;\mathrm{values}\;\mathrm{of}\;\mathrm x$

Complete step by step answer:
The graphs of the two functions are-

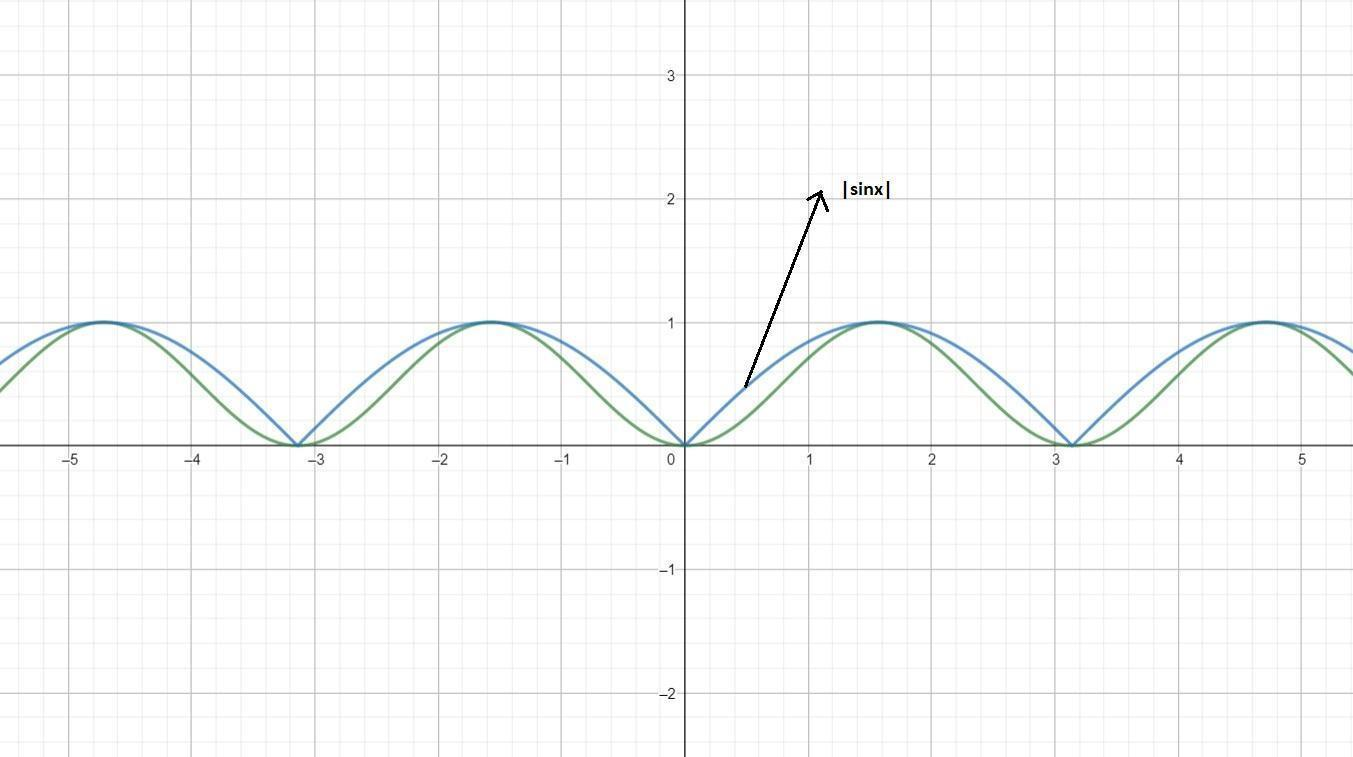
Here the the graph which is inside is $sin^2x$ and the outer one is $|sinx|$. From the graph it is clearly visible that $sin^2x$ is smooth all along but $|sinx|$ has a sharp curve when it touches the x-axis.
Since $sin^2x$ is smooth at all points, it is continuous and differentiable at every point.
Since $|sinx|$ has sharp curves when it touches the x-axis, it is neither continuous nor differentiable at those points.

This is the required answer.

Note: Initially when looking at the graph, it seems that both the functions are perfectly smooth, but it is not right. Due to the presence of modulus function, $|sinx|$ changes direction abruptly. But $sin^2x$ changes the direction in a smooth manner.