Question

Draw the graph of the cubic polynomial $f\left( x \right)={{x}^{3}}-2{{x}^{2}}$.

Answer 1

Hint: To draw the graph of this given cubic polynomial, first find out the points at which this function is attaining the value 0. Then find the maxima and minima points of this cubic polynomial by differentiating with function with respect to x and equate this derivative to 0. Then check the sign of the given polynomial around the maxima and minima by putting the points before and after the maxima and minima in the function and then see where the function is positive and negative.

Complete step by step answer:
The cubic polynomial given in the question is:
$f\left( x \right)={{x}^{3}}-2{{x}^{2}}$
First of all, we are going to find when the function is becoming 0. For this, we will equate the function equal to 0 and find the points where the function is attaining the value 0.
$f\left( x \right)={{x}^{3}}-2{{x}^{2}}=0$
Taking ${{x}^{2}}$ as common from the function then the function will look like,
${{x}^{2}}\left( x-2 \right)=0$
The value of x in the above equation where the function is attaining the value 0 is $x=0,2$.
Now, we are going to find the maxima and minima of the given polynomial by differentiating the polynomial with respect to x and then equating it to 0.
$\begin{align}
  & f\left( x \right)={{x}^{3}}-2{{x}^{2}} \\
 & f'\left( x \right)=3{{x}^{2}}-2x \\
\end{align}$
Equating the derivative to 0 we get,
$3{{x}^{2}}-2x=0$
We can see from the above equation that x can be taken out as common.
$x\left( 3x-2 \right)=0$
The solutions of the above equation are $x=0,\dfrac{3}{2}$.
So, the function is attaining maxima and minima at $x=0,\dfrac{3}{2}$.To find the maximum and minimum value substitute these values of x in the given cubic polynomial.
Substituting the value of $x=0$ in the given cubic polynomial we get,
$\begin{align}
  & f\left( x \right)={{x}^{3}}-2{{x}^{2}} \\
 & \Rightarrow f\left( 0 \right)=0-2\left( 0 \right)=0 \\
\end{align}$
Substituting the value of $x=\dfrac{3}{2}$ in the given cubic polynomial we get,
$\begin{align}
  & f\left( x \right)={{x}^{3}}-2{{x}^{2}} \\
 & \Rightarrow f\left( \dfrac{3}{2} \right)={{\left( \dfrac{3}{2} \right)}^{3}}-2{{\left( \dfrac{3}{2} \right)}^{2}} \\
 & \Rightarrow f\left( \dfrac{3}{2} \right)=\dfrac{27}{8}-\dfrac{9}{2} \\
 & f\left( \dfrac{3}{2} \right)=\dfrac{27-36}{8}=-\dfrac{9}{8} \\
\end{align}$
From the above values, we have found that the function is attaining maxima at x = 0 and minima at $x=\dfrac{3}{2}$.
We are going to find whether the maximum and minimum at these points $x=0,\dfrac{3}{2}$ is concave upwards or downwards.
Checking at $x=0$,
Putting $x=-1$ in the given function we get,
$\begin{align}
  & f\left( x \right)={{x}^{3}}-2{{x}^{2}} \\
 & f\left( -1 \right)=-1-2=-3 \\
\end{align}$
Putting $x=1$ in the given function we get,
$\begin{align}
  & f\left( x \right)={{x}^{3}}-2{{x}^{2}} \\
 & f\left( 1 \right)=1-2=-1 \\
\end{align}$
The signs of the function before and after are negative so the function is concave upwards at $x=0$.
Checking at $x=\dfrac{3}{2}$,
Putting $x=1$ in the given function we get,
$\begin{align}
  & f\left( x \right)={{x}^{3}}-2{{x}^{2}} \\
 & f\left( 1 \right)=1-2=-1 \\
\end{align}$
Putting $x=2$ in the given function we get,
$\begin{align}
  & f\left( x \right)={{x}^{3}}-2{{x}^{2}} \\
 & f\left( 2 \right)=8-8=0 \\
\end{align}$
And the value of the function at $x=\dfrac{3}{2}$ is:
$f\left( \dfrac{3}{2} \right)=-\dfrac{9}{8}$
As you can see that at $x=\dfrac{3}{2}$, the function has least value as compared to before and after $x=\dfrac{3}{2}$ so the function at this point is concave upwards.
In the below diagram, we have shown the graph of the given cubic polynomial.

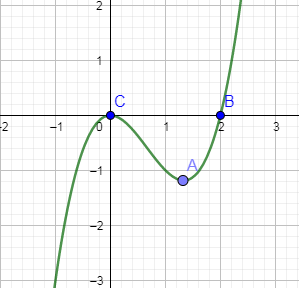
You can see from the above figure that the function is attaining the value 0 at points B & C where $x=0,2$ and the function is having maxima at point C where $x=0$ and minima at point A where $x=\dfrac{3}{2}$.

Note: You might have thought that when x is taking the extremes values i.e. $+\infty $ or $-\infty $ how the cubic polynomial behave on these extreme values which you can see by substituting $+\infty $ in the cubic polynomial then you will get the value of y as $+\infty $ and when you substitute $-\infty $ in place of x in the cubic polynomial then you will get the value of y as $-\infty $because as the degree of the cubic polynomial is odd so when you put negative value of $\infty $ then the value of y is also $-\infty $.