Question

Draw the graph of the following:
i) \[y = 0\]
ii) \[x = 5\]
iii) \[x = - 7\]
iv) \[y = 4\]
v) \[y = - 3\]

Answer 1

Hint: In the given question, we need to understand that the given equations are either of the form\[x = a\]or\[y = b\]. It represents a straight line parallel to\[y - axis\]in case of\[x = a\]and parallel to\[x - axis\]in case of\[y = b\]. So, we will draw them on a Cartesian plane.
The linear equation in one variable represents a point on a number line, a line on a Cartesian plane, and a plane on a three-dimensional plane.

Complete step by step answer:
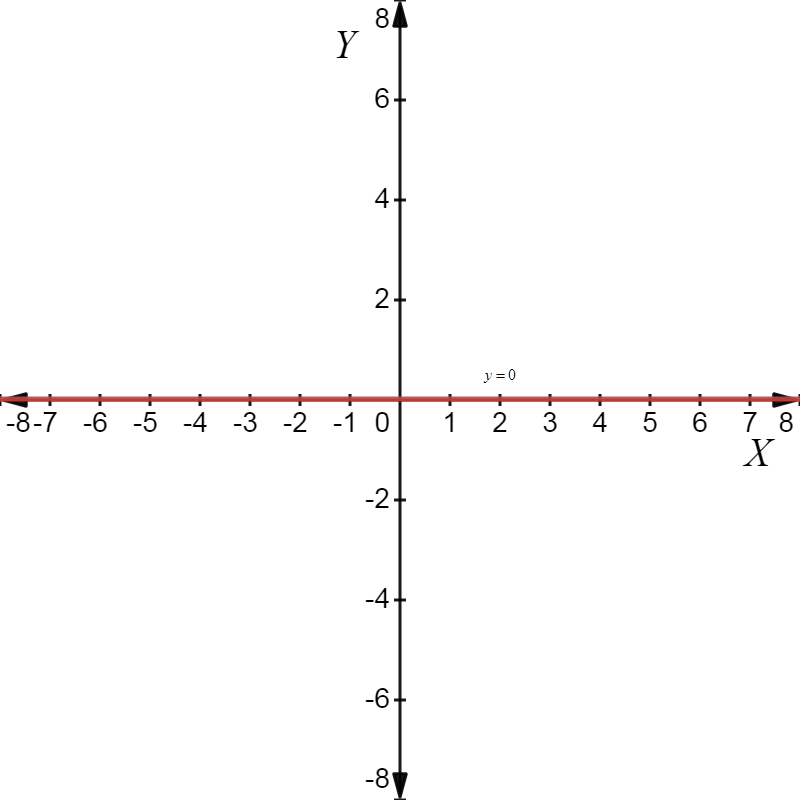
i) \[y = 0\]
This means that for every value of\[x\], would always be equal to zero.

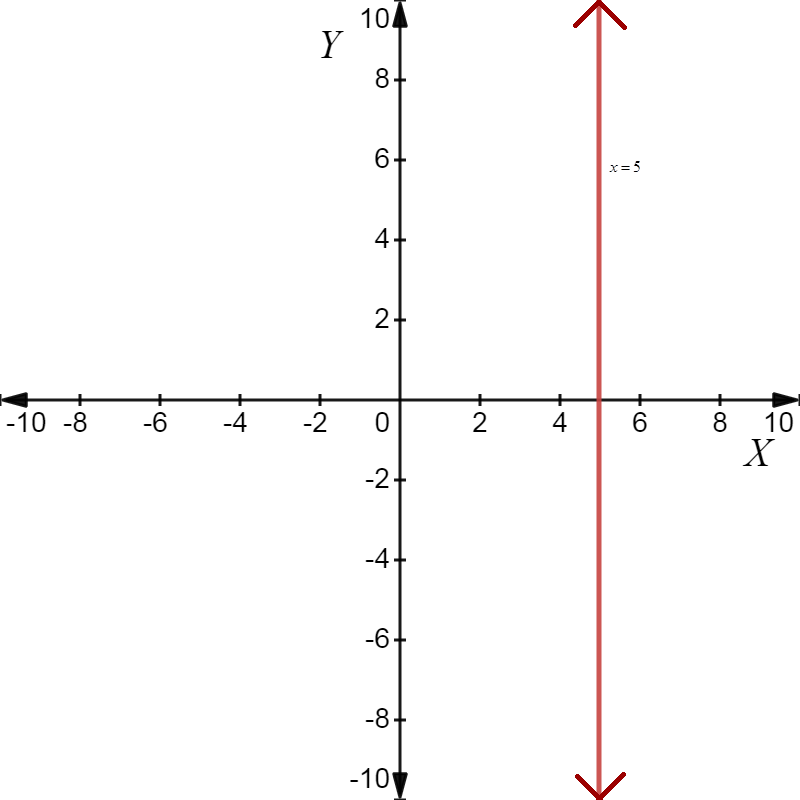
ii) \[x = 5\]
This means that the representing\[x = 5\] passes through point\[\left( {5,0} \right)\]. So, we will draw the line parallel to\[y - axis\]and pass through\[\left( {5,0} \right)\].

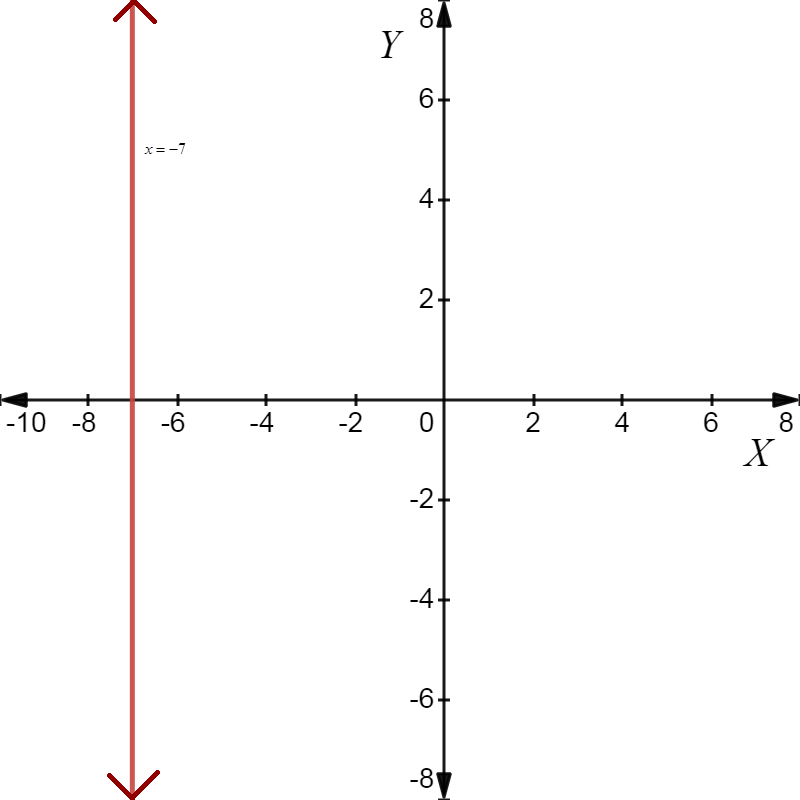
iii) \[x = - 7\]
This means that the straight line representing\[x = - 7\] passes through point\[\left( { - 7,0} \right)\]. So, we will draw the line parallel to\[y - axis\]and passing through\[\left( { - 7,0} \right)\]

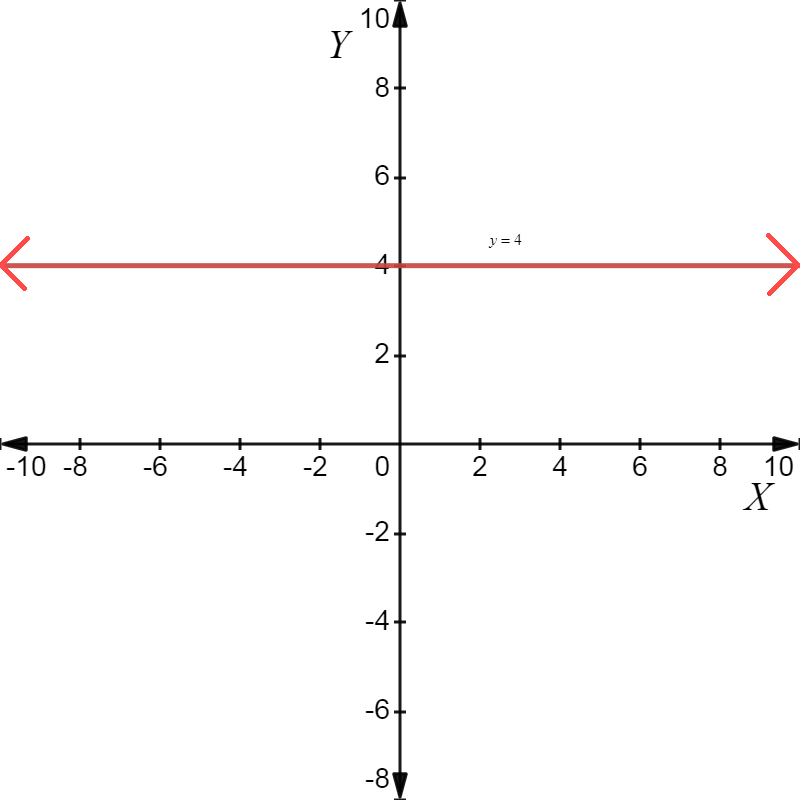
iv) \[y = 4\]
This means that the line representing\[y = 4\] passes through point\[\left( {0,4} \right)\]. So, we will draw the line parallel to\[x - axis\]and passing through\[\left( {0,4} \right)\]

v) \[y = - 3\]
This means that the line representing\[y = - 3\] passes through point\[\left( {0, - 3} \right)\]. So, we will draw the line parallel to\[x - axis\]and pass through\[\left( {0, - 3} \right)\].

Note: The linear equation in one variable is an equation which can be expressed in the form of \[ax + b = 0\], where \[a\]and \[b\]are two integers, and \[x\] is a variable and has a unique solution. To Graph the linear equations in one variable, firstly, find the \[x\]-intercept. Then plot the line which is either parallel to\[x\] axis or \[y\] axis and cutting the coordinate axis at\[\left( { \pm a,0} \right),\left( {0, \pm b} \right)\].