
Draw the graph of the following inverse trigonometric function ${{\tan }^{-1}}x$ .
Answer
590.4k+ views
Hint: For drawing the graph of ${{\tan }^{-1}}x$ first, we will see some of the fundamental concepts of functions and understand the concept of bijective functions. Then, we will draw the graph of $y=\tan x$ . After that, we will modify its domain and co-domain to make the function $y=\tan x$ invertible. Then, we will write the domain and co-domain for the function $y={{\tan }^{-1}}x$ and draw its graph.
Complete step-by-step answer:
Given:
We have to draw the plot for the function $y=f\left( x \right)={{\tan }^{-1}}x$ .
Now, before we proceed to plot the curve we should know some fundamental concepts of functions and necessary conditions for a function, so that its inverse exists.
One-one Functions:
A function $f:A\to B$ is one-one if for any $f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)\Rightarrow {{x}_{1}}={{x}_{2}}$ , i.e. the image of a distinct element of $A$ under $f$ mapping (function) are distinct. In simple words for any input value in the function there is a unique output value then, such function will be called one-one function.
Onto Functions:
A function $f:A\to B$ is onto if the range of the function $f=B$ , i.e. $f\left( A \right)=B$ , i.e. every element of $B$ is the image of some element of $A$ . In simple words the range of the function $f$ should be equal to the set of co-domain $B$ then, the function will be called onto function.
Now, functions which are both on-one and onto then, such functions are called as bijective functions. And in bijective functions, the number of elements in the domain and co-domain should be equal.
Now, as we know that corresponding to every bijection (one-one-onto function) $f:A\to B$ there exist a bijection $g:B\to A$ defined by, $g\left( y \right)=x$ if and only if $f\left( x \right)=y$ . Then, the function $g:B\to A$ is called the inverse of the function $f:A\to B$ and is denoted by ${{f}^{-1}}$ .
Thus, we have $f\left( x \right)=y\Leftrightarrow {{f}^{-1}}\left( y \right)=x$ . Then, $\left( {{f}^{-1}}of \right)\left( x \right)={{f}^{-1}}\left( f\left( x \right) \right)={{f}^{-1}}\left( y \right)=x$ , for all $x\in A$ and, $\left( fo{{f}^{-1}} \right)\left( y \right)=f\left( {{f}^{-1}}\left( y \right) \right)=f\left( x \right)=y$ , for all $y\in B$ .
Now, as we know that trigonometric functions are periodic functions and hence, in general, all trigonometric functions are not bijections. Consequently, their inverse does not exist. However, if we restrict the domains and co-domains, they can be bijective functions and we can obtain their inverses.
Now, before we draw a plot for the function $y=f\left( x \right)={{\tan }^{-1}}x$ , we should know the plot of the function $y=\tan x$ . For more clarity look at the figure given below:
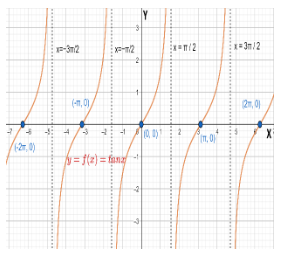
In the above figure, the general plot of the function $y=\tan x$ is shown.
Now, consider the function $f:R\to R$ given by $f\left( x \right)=\tan x$ . The graph of this function is shown in the above figure. Clearly, it is many to one onto function as it attains the same value at infinitely many points and its range $\left( -\infty ,\infty \right)$ is the same as its co-domain. In order to make $f$ a one-one function, we will have to restrict its domain in such a way that in that domain there is no turn in the graph of the function and the function takes every value between $-\infty $ and $\infty $ .
Now, it is evident from the graph of $f\left( x \right)=\tan x$ that if we take the domain as $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ then $f\left( x \right)=\tan x$ becomes one-one. Thus, $f:\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)\to \left( -\infty ,\infty \right)$ given by $f\left( x \right)=\tan x$ is a bijection and hence invertible.
Now, the inverse of $\tan $ function is denoted by ${{\tan }^{-1}}$ . Thus, ${{\tan }^{-1}}$ is a function with domain $\left( -\infty ,\infty \right)$ and range $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ such that, ${{\tan }^{-1}}x=y\Leftrightarrow \tan y=x$ .
Now, in order to plot, $y={{\tan }^{-1}}x$ we can plot $x=\tan y$ for $x\in \left( -\infty ,\infty \right)$ and $y\in \left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ . For more clarity look at the figure given below:
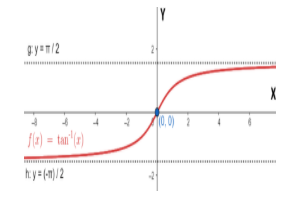
Now, the above plot is the required plot of the function $y=f\left( x \right)={{\tan }^{-1}}x$ .
Note: Here, the student should first understand how we are making a trigonometric function bijective. Then, we should remember the standard conventions that are considered for the function $y={{\tan }^{-1}}x$ and try to understand them. Moreover, we should not modify the domain and co-domain of the function as per our decision and try to learn the standard conventions.
Complete step-by-step answer:
Given:
We have to draw the plot for the function $y=f\left( x \right)={{\tan }^{-1}}x$ .
Now, before we proceed to plot the curve we should know some fundamental concepts of functions and necessary conditions for a function, so that its inverse exists.
One-one Functions:
A function $f:A\to B$ is one-one if for any $f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)\Rightarrow {{x}_{1}}={{x}_{2}}$ , i.e. the image of a distinct element of $A$ under $f$ mapping (function) are distinct. In simple words for any input value in the function there is a unique output value then, such function will be called one-one function.
Onto Functions:
A function $f:A\to B$ is onto if the range of the function $f=B$ , i.e. $f\left( A \right)=B$ , i.e. every element of $B$ is the image of some element of $A$ . In simple words the range of the function $f$ should be equal to the set of co-domain $B$ then, the function will be called onto function.
Now, functions which are both on-one and onto then, such functions are called as bijective functions. And in bijective functions, the number of elements in the domain and co-domain should be equal.
Now, as we know that corresponding to every bijection (one-one-onto function) $f:A\to B$ there exist a bijection $g:B\to A$ defined by, $g\left( y \right)=x$ if and only if $f\left( x \right)=y$ . Then, the function $g:B\to A$ is called the inverse of the function $f:A\to B$ and is denoted by ${{f}^{-1}}$ .
Thus, we have $f\left( x \right)=y\Leftrightarrow {{f}^{-1}}\left( y \right)=x$ . Then, $\left( {{f}^{-1}}of \right)\left( x \right)={{f}^{-1}}\left( f\left( x \right) \right)={{f}^{-1}}\left( y \right)=x$ , for all $x\in A$ and, $\left( fo{{f}^{-1}} \right)\left( y \right)=f\left( {{f}^{-1}}\left( y \right) \right)=f\left( x \right)=y$ , for all $y\in B$ .
Now, as we know that trigonometric functions are periodic functions and hence, in general, all trigonometric functions are not bijections. Consequently, their inverse does not exist. However, if we restrict the domains and co-domains, they can be bijective functions and we can obtain their inverses.
Now, before we draw a plot for the function $y=f\left( x \right)={{\tan }^{-1}}x$ , we should know the plot of the function $y=\tan x$ . For more clarity look at the figure given below:

In the above figure, the general plot of the function $y=\tan x$ is shown.
Now, consider the function $f:R\to R$ given by $f\left( x \right)=\tan x$ . The graph of this function is shown in the above figure. Clearly, it is many to one onto function as it attains the same value at infinitely many points and its range $\left( -\infty ,\infty \right)$ is the same as its co-domain. In order to make $f$ a one-one function, we will have to restrict its domain in such a way that in that domain there is no turn in the graph of the function and the function takes every value between $-\infty $ and $\infty $ .
Now, it is evident from the graph of $f\left( x \right)=\tan x$ that if we take the domain as $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ then $f\left( x \right)=\tan x$ becomes one-one. Thus, $f:\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)\to \left( -\infty ,\infty \right)$ given by $f\left( x \right)=\tan x$ is a bijection and hence invertible.
Now, the inverse of $\tan $ function is denoted by ${{\tan }^{-1}}$ . Thus, ${{\tan }^{-1}}$ is a function with domain $\left( -\infty ,\infty \right)$ and range $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ such that, ${{\tan }^{-1}}x=y\Leftrightarrow \tan y=x$ .
Now, in order to plot, $y={{\tan }^{-1}}x$ we can plot $x=\tan y$ for $x\in \left( -\infty ,\infty \right)$ and $y\in \left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ . For more clarity look at the figure given below:

Now, the above plot is the required plot of the function $y=f\left( x \right)={{\tan }^{-1}}x$ .
Note: Here, the student should first understand how we are making a trigonometric function bijective. Then, we should remember the standard conventions that are considered for the function $y={{\tan }^{-1}}x$ and try to understand them. Moreover, we should not modify the domain and co-domain of the function as per our decision and try to learn the standard conventions.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

How much time does it take to bleed after eating p class 12 biology CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




