
Draw the graphs of the quadratic polynomial, \[f(x)=3-2x-{{x}^{2}}\].
Answer
505.5k+ views
Hint: Put \[f(x)=y\]. Thus give x various values and get the coordinates (x, y) to plot the graph. After plotting the points, join the points with a smooth free hand curve and identify the curve that we have obtained.
Complete step by step answer:
Given us is the quadratic polynomial \[f(x)=3-2x-{{x}^{2}}\].
Let us put \[f(x)=y\].
\[\therefore y=3-2x-{{x}^{2}}\]
Now let us list a few values of \[y=3-2x-{{x}^{2}}\] corresponding to the values of x as,
Thus the following points lie on the graph of the polynomial \[y=3-2x-{{x}^{2}}\].
Thus the 11 points are (-5, -12), (-4, -5), (-3, 0), (-2, 3) (-1, 4), (0, 3), (1, 0), (2, -5), (3, -12), (4, -21), (5, -29).
Now let us plot these points on a graph paper and draw a smooth free hand arriving passing through three points to obtain the graphs of \[y=3-2x-{{x}^{2}}\].
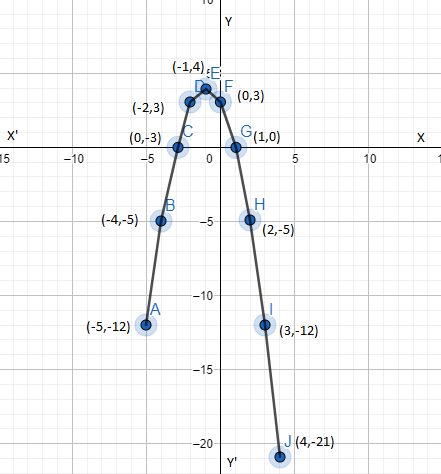
The curve thus obtained represents a parabola. The highest point P (1,-4) is called a maximum point, is the vertex of the parabola. Vertical line through P is the axis of the parabola.
Thus the parabola is symmetric about the axis.
If we factorize the polynomial \[f(x)=3-2x-{{x}^{2}}\], we get, i.e. , the product of 2 terms should be 3.
Sum of the 2 terms should be -2.
Thus we get factorized f(x) as (1-x) (x+3) which is two distinct linear factors.
So the parabola cuts x-axis at two distinct points (1,0) and (-3,0). The coordinates of three points are zeroes of f(x).
Thus we got the required parabola which is symmetric about the x-axis.
Note: The coefficient of \[{{x}^{2}}\] in \[f(x)=3-2x-{{x}^{2}}\] is 1. It is a negative real number and so the parabola opens downwards. Be careful while plotting the point, if marking the point wrong, we may get the curve it won’t be parabola.
Complete step by step answer:
Given us is the quadratic polynomial \[f(x)=3-2x-{{x}^{2}}\].
Let us put \[f(x)=y\].
\[\therefore y=3-2x-{{x}^{2}}\]
Now let us list a few values of \[y=3-2x-{{x}^{2}}\] corresponding to the values of x as,
| x | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| \[y=3-2x-{{x}^{2}}\] | -12 | -5 | 0 | 3 | 4 | 3 | 0 | -5 | -12 | -21 | -29 |
Thus the following points lie on the graph of the polynomial \[y=3-2x-{{x}^{2}}\].
Thus the 11 points are (-5, -12), (-4, -5), (-3, 0), (-2, 3) (-1, 4), (0, 3), (1, 0), (2, -5), (3, -12), (4, -21), (5, -29).
Now let us plot these points on a graph paper and draw a smooth free hand arriving passing through three points to obtain the graphs of \[y=3-2x-{{x}^{2}}\].

The curve thus obtained represents a parabola. The highest point P (1,-4) is called a maximum point, is the vertex of the parabola. Vertical line through P is the axis of the parabola.
Thus the parabola is symmetric about the axis.
If we factorize the polynomial \[f(x)=3-2x-{{x}^{2}}\], we get, i.e. , the product of 2 terms should be 3.
Sum of the 2 terms should be -2.
Thus we get factorized f(x) as (1-x) (x+3) which is two distinct linear factors.
So the parabola cuts x-axis at two distinct points (1,0) and (-3,0). The coordinates of three points are zeroes of f(x).
Thus we got the required parabola which is symmetric about the x-axis.
Note: The coefficient of \[{{x}^{2}}\] in \[f(x)=3-2x-{{x}^{2}}\] is 1. It is a negative real number and so the parabola opens downwards. Be careful while plotting the point, if marking the point wrong, we may get the curve it won’t be parabola.
Recently Updated Pages
What percentage of the area in India is covered by class 10 social science CBSE

The area of a 6m wide road outside a garden in all class 10 maths CBSE

What is the electric flux through a cube of side 1 class 10 physics CBSE

If one root of x2 x k 0 maybe the square of the other class 10 maths CBSE

The radius and height of a cylinder are in the ratio class 10 maths CBSE

An almirah is sold for 5400 Rs after allowing a discount class 10 maths CBSE

Trending doubts
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Why is there a time difference of about 5 hours between class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

Write an application to the principal requesting five class 10 english CBSE




