
Draw the histogram of the weekly pocket expenses of 125 students of a school given below. \[\]
Weekly Expenses (In Rs) No. Of students 10-20 10 20-30 15 30-50 40 50-60 25 60-90 30 90-100 5
| Weekly Expenses (In Rs) | No. Of students |
| 10-20 | 10 |
| 20-30 | 15 |
| 30-50 | 40 |
| 50-60 | 25 |
| 60-90 | 30 |
| 90-100 | 5 |
Answer
412.4k+ views
Hint: We find the width of each bin of weekly expenses by subtracting the lower limit of the bin from the upper limit as10, 10, 20, 10, 30, and 10. The frequency is the number of students in each bin which are 10, 15, 40, and 25,30,5. We draw vertical bars with width equal to width of the bins and the height equal to the corresponding frequency of the bin.
Complete step by step answer:
We know that histogram is an approximate representation of distribution of numerical data. We need a range of values called bins or intervals and the number of items that fall into a particular bin also called frequency. The bins have to be continuous, non-overlapping and most of the time equal. . \[\]
The histogram consists of adjacent vertical rectangular bars on the horizontal axis whose width is proportional to the width of the bin and height is proportional to corresponding frequency of the bin frequencies. \[\]
Let us observe the given table of the weekly pocket expenses of 125 students of a school from the question. . \[\]
We are given 7 bins of weekly expenses in rupees and their corresponding frequencies as the number of students. We see that the bins are not of equal width for example the width of first bin from the top is $20-10=10$ , the width of third bin is $50-30=20$ and the width of fifth bin is $90-60=30.$ . \[\]
Let us draw the first rectangular bar for the bin 10-20 whose width is $20-10=10$ and its frequency is 10 which will be the height of the bar. So we have figure as \[\]
We similarly find the width of other bins 20-30, 30-50, 50-60, 60-90, 90-100 as 10, 20, 10, 30, 10 respectively and the corresponding height as 10, 15, 40, 25, and 30. We draw the adjacent rectangular bars starting for the bin 20-30. We have the required histogram as \[\]
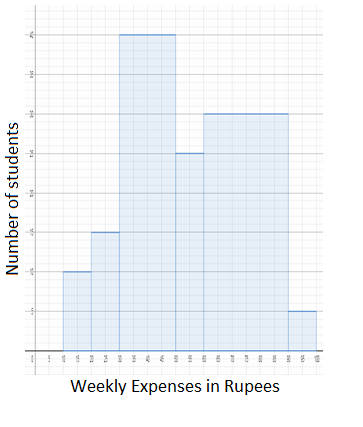
Note: We note that it is not the height but the area of the rectangular bars (width $\times $ height) that represents how much frequency is distributed within the bin. We must be careful of the confusion between histogram and bar chart. The histogram is a type of bar chart where the frequency is distributed over continuous bins as vertical bars but bar charts can also take discontinuous categories with or horizontal bars.
Complete step by step answer:
We know that histogram is an approximate representation of distribution of numerical data. We need a range of values called bins or intervals and the number of items that fall into a particular bin also called frequency. The bins have to be continuous, non-overlapping and most of the time equal. . \[\]
The histogram consists of adjacent vertical rectangular bars on the horizontal axis whose width is proportional to the width of the bin and height is proportional to corresponding frequency of the bin frequencies. \[\]
Let us observe the given table of the weekly pocket expenses of 125 students of a school from the question. . \[\]
| Weekly Expenses (In Rs) | No. Of students |
| 10-20 | 10 |
| 20-30 | 15 |
| 30-50 | 40 |
| 50-60 | 25 |
| 60-90 | 30 |
| 90-100 | 5 |
We are given 7 bins of weekly expenses in rupees and their corresponding frequencies as the number of students. We see that the bins are not of equal width for example the width of first bin from the top is $20-10=10$ , the width of third bin is $50-30=20$ and the width of fifth bin is $90-60=30.$ . \[\]
Let us draw the first rectangular bar for the bin 10-20 whose width is $20-10=10$ and its frequency is 10 which will be the height of the bar. So we have figure as \[\]

We similarly find the width of other bins 20-30, 30-50, 50-60, 60-90, 90-100 as 10, 20, 10, 30, 10 respectively and the corresponding height as 10, 15, 40, 25, and 30. We draw the adjacent rectangular bars starting for the bin 20-30. We have the required histogram as \[\]

Note: We note that it is not the height but the area of the rectangular bars (width $\times $ height) that represents how much frequency is distributed within the bin. We must be careful of the confusion between histogram and bar chart. The histogram is a type of bar chart where the frequency is distributed over continuous bins as vertical bars but bar charts can also take discontinuous categories with or horizontal bars.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
When people say No pun intended what does that mea class 8 english CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

How many ounces are in 500 mL class 8 maths CBSE

Which king started the organization of the Kumbh fair class 8 social science CBSE

Advantages and disadvantages of science

What is BLO What is the full form of BLO class 8 social science CBSE




