Question

Draw the line(s) of symmetry for each figure drawn below:

Answer 1

Hint:
We can consider the given figure as a rectangle. Then we can find the lines of symmetry of a rectangle. Then we can check whether the given diagram is also symmetric in the line of symmetry of the rectangle. Then we can draw the line of symmetries of the given figure as the line of symmetries of the rectangle that satisfy the condition. Thus, we obtain the required lines of symmetry.

Complete step by step solution:
We know that line of symmetry is the line that cuts a shape into equal two parts that can be superimposed on folding through the line.
We can see that the given figure is similar to a rectangle. We know that a rectangle has 2 lines of symmetry, one horizontally and the other one vertically. We can draw the lines of symmetry of a rectangle as follows.

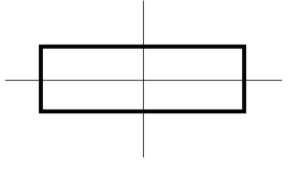
Now we can consider the vertical line of symmetry for the given figure.

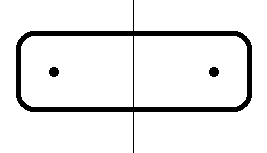
By observing the diagram, we can say that this line is a line of symmetry of the given figure.
Now we can consider the horizontal line of symmetry for the given figure.

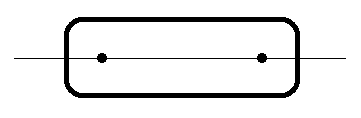
By observing the diagram, we can say that this line is a line of symmetry of the given figure.
So, we can combine the above figures to get the required lines of symmetry.

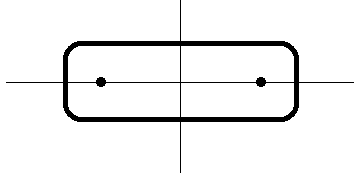
Note:
We must make sure that the lines of symmetry must pass through the mid points of the sides and through the centre of the circle. There will not be any other lines of symmetry. We need to find only the lines of symmetry, not the radial symmetry. We can confirm our solution by checking whether we will get one side of the line as the mirror image of the other side of the line.