Question

Draw the molecular orbital diagram of ${N_2},N_2^ + ,N_2^ - $. Write their electronic configuration, find the bond order and predict their magnetic behavior. Arrange the above in increasing order of bond length

Answer 1

Hint: Bond length is approximately equal to the average distance between the nuclei of two bonded atoms. More will be the bond order more will be the pull between electrons of two atoms and less will be the bond length.

Formula used: bond order$ = \dfrac{{{\text{bonding electrons - antibonding electrons}}}}{2}$


Complete step by step answer:
Molecular orbital diagram explains the chemical bonding in the molecules in terms of molecular orbital theory. In a molecular orbital diagram, the diagram of molecular orbital energy levels is shown as horizontal lines. Degenerate orbitals (orbitals having the same energy) are shown side by side in these diagrams. Electrons are filled according to the Pauli Exclusion Principle.
Basic structure of molecular orbital diagram for nitrogen is:

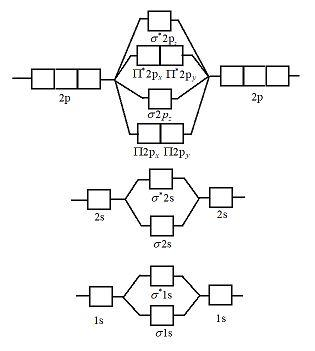\[{\text{ }}\]
Electrons of nitrogen are to be filled in this diagram. Left side represents the configuration of one atom of nitrogen molecule and the right side represents the second atom of nitrogen molecule.
Atomic number of nitrogen is seven. Therefore in ${N_2}$ there are a total fourteen electrons. Molecular orbital diagram of ${N_2}$ is shown below:

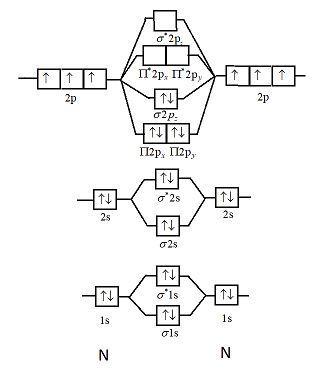
This picture shows the molecular orbital diagram of ${N_2}$. Orbitals represented by $^*$ are antibonding orbitals and the orbitals without $^*$ are bonding orbitals. Bond order can be calculated by the formula:
Bond order $ = \dfrac{{{\text{bonding electrons - antibonding electrons}}}}{2}$
In this case the number of bonding electrons is $10$ and number of antibonding electrons is $4$. Substituting the values in the formula:
Bond order $ = \dfrac{{10 - 4}}{2}$
Bond order $ = 3$
So, the bond order of nitrogen is $3$.
Electronic configuration of ${N_2}$ is: ${\left( {\sigma 1s} \right)^2}{\left( {{\sigma ^*}1s} \right)^2}{\left( {\sigma 2s} \right)^2}{\left( {{\sigma ^*}2s} \right)^2}{\left( {\Pi 2{p_x}} \right)^2}{\left( {\Pi 2{p_y}} \right)^2}{\left( {\sigma 2{p_z}} \right)^2}$
From the diagram we can see that in ${N_2}$ all the electrons are paired and hence the magnetic moment of this compound is zero.
Atomic number of nitrogen is seven. Therefore in ${N_2}$ there are a total fourteen electrons. But $N_2^ + $ has one electron less than that of nitrogen molecules. So, total electrons are thirteen. Molecular orbital diagram of $N_2^ + $ is shown below:

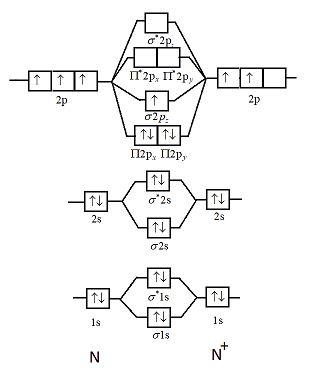
This picture shows the molecular orbital diagram of $N_2^ + $. Orbitals represented by $^*$ are antibonding orbitals and the orbitals without $^*$ are bonding orbitals. Bond order can be calculated by the formula:
Bond order $ = \dfrac{{{\text{bonding electrons - antibonding electrons}}}}{2}$
In this case the number of bonding electrons is $9$ and number of antibonding electrons is $4$. Substituting the values in the formula:
Bond order $ = \dfrac{{9 - 4}}{2}$
Bond order $ = 2.5$
So, the bond order of nitrogen is $2.5$.
Electronic configuration of $N_2^ + $ is: ${\left( {\sigma 1s} \right)^2}{\left( {{\sigma ^*}1s} \right)^2}{\left( {\sigma 2s} \right)^2}{\left( {{\sigma ^*}2s} \right)^2}{\left( {\Pi 2{p_x}} \right)^2}{\left( {\Pi 2{p_y}} \right)^2}\left( {\sigma 2{p_z}} \right)$
From the diagram we can see that in $N_2^ + $ only one electron is unpaired. So, it will have some net magnetic moment.
Atomic number of nitrogen is seven. Therefore in ${N_2}$ there are a total fourteen electrons. But $N_2^ - $ has one electron more than that of nitrogen molecule. So, total electrons are fifteen. Molecular orbital diagram of $N_2^ - $ is shown below:

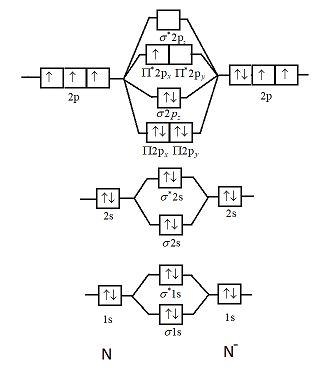
This picture shows the molecular orbital diagram of $N_2^ - $. Orbitals represented by $^*$ are antibonding orbitals and the orbitals without $^*$ are bonding orbitals. Bond order can be calculated by the formula:
Bond order $ = \dfrac{{{\text{bonding electrons - antibonding electrons}}}}{2}$
In this case the number of bonding electrons is $10$ and number of antibonding electrons is $5$. Substituting the values in the formula:
Bond order $ = \dfrac{{10 - 5}}{2}$
Bond order $ = 2.5$
So, the bond order of nitrogen is $2.5$.
Electronic configuration of $N_2^ - $ is: ${\left( {\sigma 1s} \right)^2}{\left( {{\sigma ^*}1s} \right)^2}{\left( {\sigma 2s} \right)^2}{\left( {{\sigma ^*}2s} \right)^2}{\left( {\Pi 2{p_x}} \right)^2}{\left( {\Pi 2{p_y}} \right)^2}{\left( {\sigma 2{p_z}} \right)^2}\left( {{\Pi ^*}2{p_x}} \right)$
From the diagram we can see that in $N_2^ - $ only one electron is unpaired. So, it will have some net magnetic moment.
We know more will be the bond order less will be the bond length. Among the given molecules, ${N_2}$ has the highest bond order. So, the bond length of ${N_2}$ will be shortest. Bond order of $N_2^ + {\text{ and }}N_2^ - $ is same but number of antibonding electrons in $N_2^ - $ is more so, it will make weaker bond as compared to $N_2^ + $. So, correct order of bond length is:
$N_2^ - > N_2^ + > {N_2}$

Note:
Molecules which have unpaired electrons have net magnetic moment and are called paramagnetic. A molecule which doesn’t have unpaired electrons that molecule does not have net magnetic moment and are called diamagnetic.