Question

Each of the exterior angles of a pentagon are in the ratio 2 : 1 : 4 : 3 : 5. Find each of the angles of the pentagon.

Answer 1

Hint: In order to find each of the interior angles of the pentagon, we consider the ratio of the exterior angles, multiply them with a variable and add all of them. They equate to 360° as a pentagon is a regular polygon. We find the actual exterior angles and subtract each of them from 180° to find the respective interior angle.

Complete step-by-step answer:
Given Data,
A pentagon
Ratio of exterior angles = 2 : 1 : 4 : 3 : 5

We know the sum of all the exterior angles of any regular polygon is always 360°. Since pentagon is also a regular polygon its sum of exterior angles is 360°.
Given the exterior angles are in the ratio 2 : 1 : 4 : 3 : 5, let us multiply them with a variable ‘K’.
Therefore the exterior angles are 2K, 1K, 4K, 3K and 5K.
The sum of exterior angles = 2K + 1K + 4K + 3K + 5K = 360°
⟹15K = 360°
⟹K = 24°

Therefore the individual exterior angles are 2(24°), 1(24°), 4(24°), 3(24°) and 5(24°).
⟹The exterior angles are 48°, 24°, 96°, 72° and 120° respectively.

Now if we look at the figure of a pentagon, the interior angle and its respective exterior angle lie on the same straight line and make up to an angle of 180°.
Angle on a straight line is 180°.

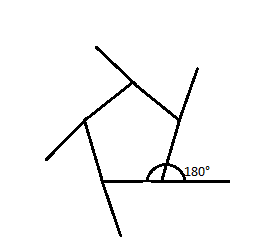
Therefore the respective interior angles to each of the exterior angles of the pentagon, 48°, 24°, 96°, 72° and 120° are:
180° - 48° = 132°
180° - 24° = 156°
180° - 96° = 84°
180° - 72° = 108°
180° - 120° = 60°
Therefore the interior angles of the pentagon are 132°, 156°, 84°, 108° and 60°.

Note: In order to solve this type of question the key is to know that all the exterior angles of a regular polygon have a sum of 360° and sum of angles on a straight line are 180°.
We can also verify the obtained answer by using the concept, sum of all interior angles in a polygon is (n – 2) × 180°, where n is the number of sides of a polygon. As the given polygon is a pentagon, n is 5. Therefore the sum of interior angles should be (5 - 2) × 180° = 540°. The sum of all the interior angles obtained is 132° + 156° + 84° + 108° + 60° = 540°. Hence the obtained values of interior angles are true.