Question

What is the effect on temperature vs time graph when the temperature of the enclosure is large in the experiment to plot the cooling curve for the relationship between the temperature of a hot body and time?
A. Graph becomes more flattened
B. Graph becomes a straight line
C. Graph becomes more curved
D. None of these.

Answer 1

Hint: Newton was the first successful person to compute the relation between temperature variation and time. However, his thesis was limited only for some special type of system in which certain assumptions were made. The assumptions made so that the law is valid are that the temperature difference of the body must not be very large and the time of consideration of the variation also must be small. This law is called Newton’s law of cooling.
Formula used: $\dfrac{dT}{dt} = - k (T - T_s)$

Complete step-by-step solution:
Newton’s law of cooling has many statements as per the conditions provided. One such statement is$\dfrac{dT}{dt} = - k (T - T_s)$. This is a statement derived from Stephen-Boltzmann’s law which relates the power radiation from a body at a particular temperature. But to come to this result, we usually assume that the temperature of the surroundings is constant and not much variable.
Now, according to the question statement, if we consider the temperature of the surrounding (enclosure) to be large, then the significance of ‘$T$’ will go on decreasing with respect to ‘$T_S$’. Hence the equation will eventually become:
$\dfrac{dT}{dt} = - k ( - T_s) = kT_S$
Hence solving the differential equation,
$dT = k T_S dt$
$\int dT = \int k T_S dt$
$\Rightarrow \int dT = k T_S \int dt$
$\Rightarrow T = k T_S t+c$
$\Rightarrow T = c_1 t+c$

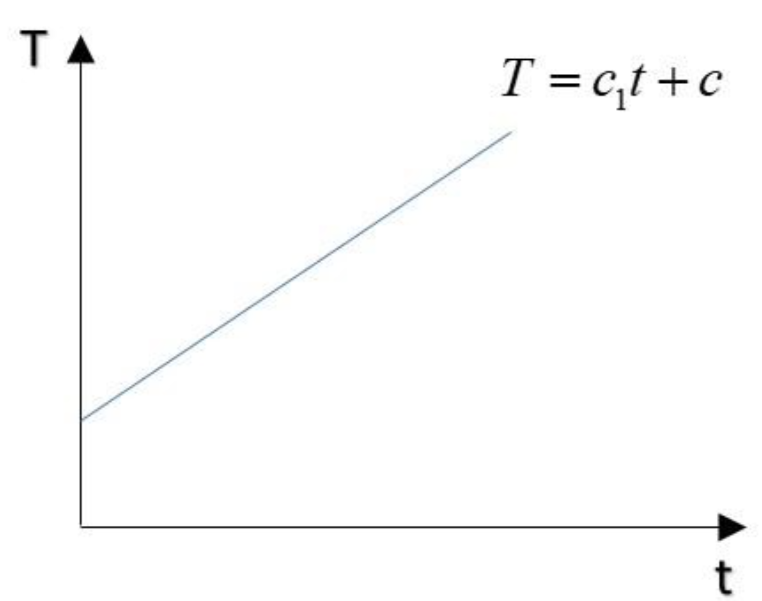
Where $c_1\ and \ c$ are constants. Hence the above equation represents the equation of a straight line. Hence according to question, the curve will become more flattened, option A. is correct.

Note: If the temperature is calculated by using this form of Newton’s law of cooling, the results will not be exactly as we’ve assumed several assumptions before deriving it. Also ‘k’ is a constant in this equation. But actually, it depends upon certain factors. In fact $k =\dfrac{ 4\sigma eAT_{\circ}^3}{ms}$ [where symbols have its usual meaning] depends upon the surrounding temperature also. So ‘k’ is constant only till the surrounding is not changed.