Question

Electric field at the centre of a quarter circular ring having charge density $\lambda$ is:

Answer 1

Hint: Here, it is important to note that the charge is distributed over an object. Hence we can’t directly apply Coulomb's law which is valid for point charge. Hence we need to get the electric field due to any general element and then integrate over the ring to get a net electric field at the centre.
Formula used:
$dE = \dfrac{Kdq}{r^2}$

Complete answer:
First of all, we have to consider an elementary part of the ring at an angle $\theta$ having angular length of $d\theta$. The small charge inside the elementary part will be calculated as follows:
Charge density $\lambda$ is defined as charge per unit length. Thus, the charge in the elementary part ‘$Rd\theta$’ will be $\lambda Rd\theta$.
Thus $dq = \lambda Rd\theta$
Now, using $dE = \dfrac{Kdq}{r^2}$, we have
$dE = \dfrac{K\lambda R d\theta}{R^2} = \dfrac{K\lambda d\theta}{R}$
Now, as the ring is unsymmetric, we have to find the field in both directions i.e. in x direction and in y direction separately.

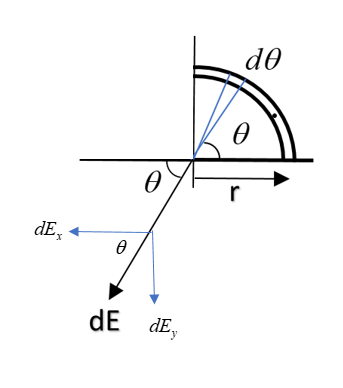
So, field in x-direction: $dE_x = dE cos \theta$
$dE_x = \dfrac{K\lambda cos\theta d\theta}{R}$
Integrating, we get:
$\int dE_x = \int \limits_{0}^{\pi /2} \dfrac{K\lambda}{R}cos\theta d\theta$
$E_x = \dfrac{K\lambda}{R}\int \limits_{0}^{\pi /2} cos\theta d\theta = \dfrac{K\lambda}{R}\left( sin(\dfrac{\pi}{2}) - sin 0 \right) = \dfrac{K\lambda}{R}$
Also, field in y-direction:
$dE_{y} = dE sin\theta = \dfrac{K\lambda}{R}\times sin\theta d\theta$
Then, $E_{y} = \int dE sin\theta= \int \dfrac{K\lambda}{ R} \times sin\theta d\theta$
Or, ${{E}_{y}}=\frac{K\lambda}{ {{R}{}}}\times \int\limits_{0}^{\pi/2 }{sin\theta {d}}\theta$ [ as K. q and r are constants ]
${{E}_{y}}=\frac{K\lambda}{ {{R}{}}}\times -\left(cos(\pi/2) - cos 0\right) = \dfrac{K\lambda}{R}$
Now, the net field will be the vector sum of both x and y component:
Thus, $E_{net} = \sqrt{E_x^2+E_y^2}$
Or $E_{net} = \sqrt{\left(\dfrac{K\lambda}R\right)^2+\left(\dfrac{K\lambda}R\right)^2}$
$\implies E_{net} = \sqrt2 \dfrac{K\lambda}{R}$

Note:
This type of question must be tackled only by taking a small element and writing electric fields for smaller elements. In some questions, the figure might be symmetric. In that case, we can directly write the component of the electric field which is symmetric as zero. Also students should understand how to take the limits. If the material were present in the first as well as second quadrant, we might have taken the limits from 0 to $\pi$ instead of 0 to$\dfrac{\pi}{2}$.