Question

What is the electric field intensity at the centroid of an equilateral triangle carrying an equal charge q at each of the vertices?
(A) Zero
(B) $ \dfrac{{\sqrt 2 kq}}{{{r^2}}} $
(C) $ \dfrac{{kq}}{{\sqrt 2 {r^2}}} $
(D) $ \dfrac{{3kq}}{{{r^2}}} $

Answer 1

Hint
The electric field from positive charges moves outwards. For equally distant charges, the electric field intensity at an equally distant point is the same.

Complete step by step answer
Electric field is the physical force on a point exerted by a charge. The field lines tend to move outwards from a positive charge, while for a negative charge they go in. It can be imagined as a loop of flow from the positive to the negative charge. The stronger the electric fields at one point, the stronger is the electrical force experienced there.
In this question, we are asked to find the electric field intensity at the centroid of an equilateral triangle. A positive charge $ q $ is placed at each of the vertices. As you can see, all the charges are equally distant from each other as they are in the formation of an equilateral triangle. The point at which we have to find the electric field intensity is also equally distant as it is the centroid of the triangle.

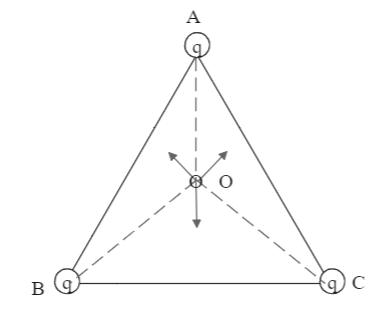
In other words, this 3-charge system would look the same no matter how we turn it. Because of the similar properties, the force exerted by each charge on the centroid O would be the same. As these are positive charges, the direction of the field would be outwards and towards the midpoint of the opposite lines. For example, the field by charge at point A would be directed towards the midpoint of line BC. The same goes for all other charges.
As the magnitude of electric field intensity remains the same for all the three charges, the only thing to take care of now is the direction. The three vectors would form a triad, consequently.
We know that the electric fields in the form of a triad cancel each other. Hence, the total electric field at the centroid O would be zero.
Thus, the answer is option (C).

Note
As we saw, charge systems that have symmetry are mostly very easy to solve. Many times the charges cancel out each other because of opposite directions and equal magnitudes. Recognising this symmetry helps reduce a lot of calculation work.