Question

What is the electric potential at the centre of a hemisphere of radius R and having surface charge density \[\sigma \]?

Answer 1

Hint: A sphere is a three-dimensional geometric object that is the surface of a ball (viz., analogous to the circular objects in two dimensions, where a "circle" circumscribes its "disk"). A spherical shell is a three-dimensional generalisation of an annulus in geometry. It's the space between two concentric circles of different radii that a ball occupies.

Complete answer:
The electric potential (also known as the electric field potential, potential decrease, or electrostatic potential) is the amount of work energy used to transfer a unit of electric charge from a reference point to a particular point in an electric field while avoiding producing.

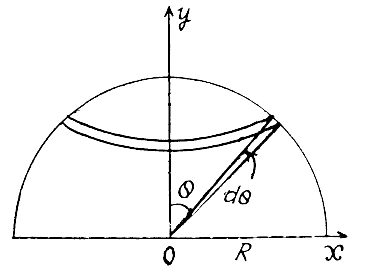
Consider the ring factor depicted in the diagram. The factor then carries the charge.
\[dq = (2\pi R\sin \theta )Rd\theta \sigma \]
As a result, the potential due to the considered element at the hemisphere's core,
\[d\varphi = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{dq}}{R} = \dfrac{{2\pi \sigma R\sin \theta d\theta }}{{4\pi {\varepsilon _0}}}\]
\[ = \dfrac{{\sigma R}}{{2{\varepsilon _0}}}\sin \theta d\theta \]
As a result of the whole hemisphere's potential
\[\varphi = \dfrac{{R\sigma }}{{2{\varepsilon _0}}}\int_0^{\pi /2} {\sin } \theta d\theta = \dfrac{{\sigma R}}{{2{\varepsilon _0}}}\]
As a result of the problem's symmetry, the hemisphere's net electric field is now oriented towards the negative y-axis. We've got
\[d{E_y} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{dq\cos \theta }}{{{R^2}}} = \dfrac{\sigma }{{2{\varepsilon _0}}}\sin \theta \cos \theta d\theta \]
\[E = E_y^\prime = \dfrac{\sigma }{{2{\varepsilon _0}}}\int_0^{\pi /2} {\sin } \theta \cos \theta d\theta \]
= \[\dfrac{\sigma }{{4{\varepsilon _0}}}\int_0^{\pi /2} {\sin } 2\theta d\theta = \dfrac{\sigma }{{4{\varepsilon _0}}},{\text{ along }}YO\]
The number of the potentials due to two identical hemispheres can be written as the potential at the centre of a spherical shell.
\[{{\mathbf{V}}_{{\text{total }}}} = {{\mathbf{V}}_{{\text{hemisphere}}{{\text{ }}_1}}} + {{\mathbf{V}}_{{\text{hemisphere}}{{\text{ }}_2}}}\]
\[{{\text{V}}_{{\text{total }}}} = 2\;{{\text{V}}_{{\text{hemisphere }}}}\]
\[ \Rightarrow \dfrac{\sigma }{{{_0}}}{\mathbf{R}} = 2\;{{\text{V}}_{{\text{hemisphere }}}}\]
\[ \Rightarrow {{\mathbf{V}}_{{\text{hemisphere }}}} = \dfrac{\sigma }{{2{_0}}}{\mathbf{R}}\]

Note: When time-varying fields are present in electrodynamics, the electric field cannot be represented solely in terms of a scalar potential. Instead, both the scalar electric potential and the magnetic vector potential can be used to express the electric field. Since the electric potential and the magnetic vector potential combine to form a four-vector, Lorentz transformations merge the two types of potential.