
Equations of perpendicular bisectors of side AB and AC of a triangle ABC are \[x-y+5=0\] and \[x+2y=0\]. If the vertex A (1, -2), then find the equation of side BC.
Answer
481.8k+ views
Hint: To solve this question we will first compute mid – points of side AB & AC of \[\Delta ABC\] and that can be calculated as line, \[x-y+5=0\] and \[x+2y=0\] are perpendicular bisectors. So, the point in mid – point of AB & AC. After computing D & E mid – points of AB & AC we will compute co – ordinates of B and C using slope of line \[x+y+c=0\] as \[\dfrac{dy}{dx}=\dfrac{-y}{x}\]. Also we will use the product by two slopes of perpendicular line is -1.
Complete step by step answer:
Let us first construct \[\Delta ABC\],
The co – ordinates of A are (1, -2).
And let D and E be the points on line AB & AC on which perpendicular bisectors are drawn.
The equation of line at D is \[x-y+5=0\] and the equation of line at E is \[x+2y=0\].
Let the co – ordinates of B be \[\left( {{x}_{1}},{{y}_{1}} \right)\] and the co – ordinates of C be \[\left( {{x}_{2}},{{y}_{2}} \right)\].
Because the perpendicular bisector of side AB is at D then D is mid – point of side AB.
\[\Rightarrow \] Co – ordinates of D = \[\left( \dfrac{1+{{x}_{1}}}{2},\dfrac{{{y}_{1}}-2}{2} \right)\].
Similarly E is also mid – point of side AC,
\[\Rightarrow \] Co – ordinates of D = \[\left( \dfrac{{{x}_{2}}+1}{2},\dfrac{{{y}_{2}}-2}{2} \right)\]
As D lies on the line \[x-y+5=0\].
So its co – ordinates satisfy the equation \[x-y+5=0\].
Substituting \[x=\dfrac{1+{{x}_{1}}}{2}\] and \[y=\dfrac{{{y}_{1}}-2}{2}\] we get,
\[\begin{align}
& \left( \dfrac{1+{{x}_{1}}}{2} \right)-\left( \dfrac{{{y}_{1}}-2}{2} \right)+5=0 \\
& \Rightarrow 1+{{x}_{1}}-{{y}_{1}}+2+10=0 \\
\end{align}\]
\[\Rightarrow {{x}_{1}}-{{y}_{1}}+13=0\] - (1)
Similarly as E lies on the line \[x+2y=0\].
\[\Rightarrow \] Co – ordinates of E satisfy \[x+2y=0\].
Substituting \[x=\dfrac{1+{{x}_{2}}}{2}\] and \[y=\dfrac{{{y}_{2}}-2}{2}\] we get,
\[\begin{align}
& \left( \dfrac{{{x}_{2}}+1}{2} \right)+2\left( \dfrac{{{y}_{2}}-2}{2} \right)=0 \\
& \Rightarrow \dfrac{{{x}_{2}}+1}{2}+{{y}_{2}}-2=0 \\
& \Rightarrow {{x}_{2}}+1+2{{y}_{2}}-4=0 \\
\end{align}\]
\[\Rightarrow {{x}_{2}}+2{{y}_{2}}-3=0\] - (2)
Now the slope of an equation \[ax+by+c=0\] is given by \[\dfrac{dy}{dx}\].
Then slope of line \[x-y+5=0\] is obtained by differentiating,
\[x-y+5=0\]
Differentiating with respect to x we have,
\[1-\dfrac{dy}{dx}+0=0\]
\[\Rightarrow \dfrac{dy}{dx}=1\] = slope of line \[x-y+5=0\].
Similarly slope of line \[x+2y=0\].
\[1+2\dfrac{dy}{dx}=0\]
\[\Rightarrow \dfrac{dy}{dx}=\dfrac{-1}{2}\] = slope of line \[x+2y=0\].
Now we will find the slope of line AB and of AC.
When co – ordinates of two points are \[\left( {{x}_{1}},{{y}_{1}} \right)\] & \[\left( {{x}_{2}},{{y}_{2}} \right)\].
Then slope is \[\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\].
Applying this we have slope of line AB is, \[\dfrac{{{y}_{2}}+2}{{{x}_{1}}-1}\].
Now because two lines which are perpendicular have the product of slopes as ‘-1’.
Then as AB and line \[x-y+5=0\] are perpendicular,
\[\Rightarrow \] (slope of AB) \[\times \] (slope of \[x-y+5=0\]) = -1
\[\Rightarrow \left( \dfrac{{{y}_{1}}+2}{{{x}_{1}}-1} \right)\left( 1 \right)=-1\]
\[\Rightarrow {{y}_{1}}-2=-{{x}_{1}}+1\Rightarrow {{x}_{1}}+{{y}_{1}}-1=0\] - (3)
Similarly slope of line AC is \[\dfrac{{{y}_{2}}+2}{{{x}_{2}}-1}\] and as both lines AC and \[x+2y=0\] are perpendicular then,
(slope of AC) \[\times \] (slope of \[x+2y=0\]) = -1
\[\Rightarrow \left( \dfrac{{{y}_{2}}+2}{{{x}_{2}}-1} \right)\times \left( \dfrac{-1}{2} \right)=-1\]
\[\Rightarrow {{y}_{2}}+2=2\left( {{x}_{2}}-1 \right)\Rightarrow 2{{x}_{\partial 2}}-{{y}_{2}}-4=0\] - (4)
Solving equation (2) and equation (3) we have,
\[{{x}_{1}}-{{y}_{1}}+13=0\]
\[\underline{{{x}_{1}}+{{y}_{1}}+1=0}\]
\[2{{x}_{1}}+14=0\]
\[{{x}_{1}}=\dfrac{-14}{2}=-7\]
\[\Rightarrow {{x}_{1}}=-7\] and \[{{y}_{1}}=6\].
Similarly solving equation (2) and equation (4) we have,
\[\begin{align}
& {{x}_{2}}+2{{y}_{2}}-3=0 \\
& 2{{x}_{2}}-{{y}_{2}}-4=0 \\
\end{align}\]
Multiplying equation (2) by 2 and substituting from equation (4) we get,
\[\begin{align}
& 2{{x}_{2}}+4{{y}_{2}}-6=0 \\
& \underline{\begin{align}
& 2{{x}_{2}}-{{y}_{2}}-4=0 \\
& ++ \\
\end{align}} \\
& +5{{y}_{2}}-2=0\Rightarrow +5{{y}_{2}}-2=0 \\
\end{align}\]
\[\Rightarrow {{y}_{2}}=\dfrac{+2}{5}\] and \[{{x}_{2}}=\dfrac{11}{5}\].
Thus co – ordinates of C are \[\left( \dfrac{11}{5},\dfrac{2}{5} \right)\].
Then equation of line BC is
\[\begin{align}
& y-6=\dfrac{\dfrac{2}{5}-6}{\dfrac{11}{5}+7}\left( x+7 \right) \\
& \Rightarrow y-6=\dfrac{-28}{46}\left( x+7 \right) \\
& \Rightarrow 14x+23y-40=0 \\
\end{align}\]
\[\therefore \] Equation of line BC is \[14x+23y-40=0\].
Note:
The key point to note here in this question is that while calculating the equation of line BC this formula is used. If \[B=\left( \alpha ,\beta \right)\] and \[C=\left( \alpha ',\beta ' \right)\] then BC = \[y-\alpha =\dfrac{\beta '-\beta }{\alpha '-\alpha }\left( x-\alpha \right)\].
Another point to note here is that slope of both lines \[x+2y=0\] and \[x-y+5=0\] is important and are used as \[\dfrac{dy}{dx}=m\] = slope of line.
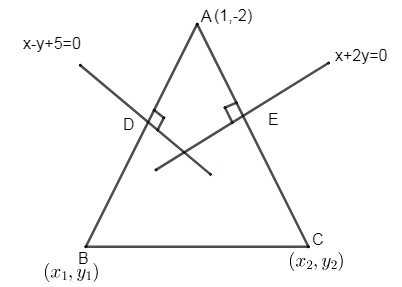
Complete step by step answer:
Let us first construct \[\Delta ABC\],

The co – ordinates of A are (1, -2).
And let D and E be the points on line AB & AC on which perpendicular bisectors are drawn.
The equation of line at D is \[x-y+5=0\] and the equation of line at E is \[x+2y=0\].
Let the co – ordinates of B be \[\left( {{x}_{1}},{{y}_{1}} \right)\] and the co – ordinates of C be \[\left( {{x}_{2}},{{y}_{2}} \right)\].

Because the perpendicular bisector of side AB is at D then D is mid – point of side AB.
\[\Rightarrow \] Co – ordinates of D = \[\left( \dfrac{1+{{x}_{1}}}{2},\dfrac{{{y}_{1}}-2}{2} \right)\].
Similarly E is also mid – point of side AC,
\[\Rightarrow \] Co – ordinates of D = \[\left( \dfrac{{{x}_{2}}+1}{2},\dfrac{{{y}_{2}}-2}{2} \right)\]
As D lies on the line \[x-y+5=0\].
So its co – ordinates satisfy the equation \[x-y+5=0\].
Substituting \[x=\dfrac{1+{{x}_{1}}}{2}\] and \[y=\dfrac{{{y}_{1}}-2}{2}\] we get,
\[\begin{align}
& \left( \dfrac{1+{{x}_{1}}}{2} \right)-\left( \dfrac{{{y}_{1}}-2}{2} \right)+5=0 \\
& \Rightarrow 1+{{x}_{1}}-{{y}_{1}}+2+10=0 \\
\end{align}\]
\[\Rightarrow {{x}_{1}}-{{y}_{1}}+13=0\] - (1)
Similarly as E lies on the line \[x+2y=0\].
\[\Rightarrow \] Co – ordinates of E satisfy \[x+2y=0\].
Substituting \[x=\dfrac{1+{{x}_{2}}}{2}\] and \[y=\dfrac{{{y}_{2}}-2}{2}\] we get,
\[\begin{align}
& \left( \dfrac{{{x}_{2}}+1}{2} \right)+2\left( \dfrac{{{y}_{2}}-2}{2} \right)=0 \\
& \Rightarrow \dfrac{{{x}_{2}}+1}{2}+{{y}_{2}}-2=0 \\
& \Rightarrow {{x}_{2}}+1+2{{y}_{2}}-4=0 \\
\end{align}\]
\[\Rightarrow {{x}_{2}}+2{{y}_{2}}-3=0\] - (2)
Now the slope of an equation \[ax+by+c=0\] is given by \[\dfrac{dy}{dx}\].
Then slope of line \[x-y+5=0\] is obtained by differentiating,
\[x-y+5=0\]
Differentiating with respect to x we have,
\[1-\dfrac{dy}{dx}+0=0\]
\[\Rightarrow \dfrac{dy}{dx}=1\] = slope of line \[x-y+5=0\].
Similarly slope of line \[x+2y=0\].
\[1+2\dfrac{dy}{dx}=0\]
\[\Rightarrow \dfrac{dy}{dx}=\dfrac{-1}{2}\] = slope of line \[x+2y=0\].
Now we will find the slope of line AB and of AC.
When co – ordinates of two points are \[\left( {{x}_{1}},{{y}_{1}} \right)\] & \[\left( {{x}_{2}},{{y}_{2}} \right)\].
Then slope is \[\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\].
Applying this we have slope of line AB is, \[\dfrac{{{y}_{2}}+2}{{{x}_{1}}-1}\].
Now because two lines which are perpendicular have the product of slopes as ‘-1’.
Then as AB and line \[x-y+5=0\] are perpendicular,
\[\Rightarrow \] (slope of AB) \[\times \] (slope of \[x-y+5=0\]) = -1
\[\Rightarrow \left( \dfrac{{{y}_{1}}+2}{{{x}_{1}}-1} \right)\left( 1 \right)=-1\]
\[\Rightarrow {{y}_{1}}-2=-{{x}_{1}}+1\Rightarrow {{x}_{1}}+{{y}_{1}}-1=0\] - (3)
Similarly slope of line AC is \[\dfrac{{{y}_{2}}+2}{{{x}_{2}}-1}\] and as both lines AC and \[x+2y=0\] are perpendicular then,
(slope of AC) \[\times \] (slope of \[x+2y=0\]) = -1
\[\Rightarrow \left( \dfrac{{{y}_{2}}+2}{{{x}_{2}}-1} \right)\times \left( \dfrac{-1}{2} \right)=-1\]
\[\Rightarrow {{y}_{2}}+2=2\left( {{x}_{2}}-1 \right)\Rightarrow 2{{x}_{\partial 2}}-{{y}_{2}}-4=0\] - (4)
Solving equation (2) and equation (3) we have,
\[{{x}_{1}}-{{y}_{1}}+13=0\]
\[\underline{{{x}_{1}}+{{y}_{1}}+1=0}\]
\[2{{x}_{1}}+14=0\]
\[{{x}_{1}}=\dfrac{-14}{2}=-7\]
\[\Rightarrow {{x}_{1}}=-7\] and \[{{y}_{1}}=6\].
Similarly solving equation (2) and equation (4) we have,
\[\begin{align}
& {{x}_{2}}+2{{y}_{2}}-3=0 \\
& 2{{x}_{2}}-{{y}_{2}}-4=0 \\
\end{align}\]
Multiplying equation (2) by 2 and substituting from equation (4) we get,
\[\begin{align}
& 2{{x}_{2}}+4{{y}_{2}}-6=0 \\
& \underline{\begin{align}
& 2{{x}_{2}}-{{y}_{2}}-4=0 \\
& ++ \\
\end{align}} \\
& +5{{y}_{2}}-2=0\Rightarrow +5{{y}_{2}}-2=0 \\
\end{align}\]
\[\Rightarrow {{y}_{2}}=\dfrac{+2}{5}\] and \[{{x}_{2}}=\dfrac{11}{5}\].
Thus co – ordinates of C are \[\left( \dfrac{11}{5},\dfrac{2}{5} \right)\].
Then equation of line BC is
\[\begin{align}
& y-6=\dfrac{\dfrac{2}{5}-6}{\dfrac{11}{5}+7}\left( x+7 \right) \\
& \Rightarrow y-6=\dfrac{-28}{46}\left( x+7 \right) \\
& \Rightarrow 14x+23y-40=0 \\
\end{align}\]
\[\therefore \] Equation of line BC is \[14x+23y-40=0\].
Note:
The key point to note here in this question is that while calculating the equation of line BC this formula is used. If \[B=\left( \alpha ,\beta \right)\] and \[C=\left( \alpha ',\beta ' \right)\] then BC = \[y-\alpha =\dfrac{\beta '-\beta }{\alpha '-\alpha }\left( x-\alpha \right)\].
Another point to note here is that slope of both lines \[x+2y=0\] and \[x-y+5=0\] is important and are used as \[\dfrac{dy}{dx}=m\] = slope of line.
Recently Updated Pages
What percentage of the area in India is covered by class 10 social science CBSE

The area of a 6m wide road outside a garden in all class 10 maths CBSE

What is the electric flux through a cube of side 1 class 10 physics CBSE

If one root of x2 x k 0 maybe the square of the other class 10 maths CBSE

The radius and height of a cylinder are in the ratio class 10 maths CBSE

An almirah is sold for 5400 Rs after allowing a discount class 10 maths CBSE

Trending doubts
For Frost what do fire and ice stand for Here are some class 10 english CBSE

What did the military generals do How did their attitude class 10 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What did being free mean to Mandela as a boy and as class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What did Valli find about the bus journey How did she class 10 english CBSE




