Question

How do you evaluate the definite integral \[\int{\left| {{x}^{2}}-4x+3 \right|dx}\] from \[\left[ 0,4 \right]\]?

Answer 1

Hint: Assume \[f\left( x \right)={{x}^{2}}-4x+3\] and factorize this quadratic equation using the middle term split method. Substitute them equal to 0 and find the values of x. Represent these obtained values of x on the number line and mark the given interval also on the same number line. Now, remove the modulus sign and break the integral into certain parts by checking the sign of the function in the interval and hence find the value of the integral given.

Complete step-by-step solution:
Here, we have been provided with the integral \[\int{\left| {{x}^{2}}-4x+3 \right|dx}\] with the limits \[\left[ 0,4 \right]\] and we are asked to find the value of this integral. Let us assume this integral as I, so we have,
\[\Rightarrow I=\int\limits_{0}^{4}{\left| {{x}^{2}}-4x+3 \right|dx}\]
To solve this integral we need to remove the modulus sign from the given quadratic function. So, using the middle term split method we have,
\[\begin{align}
  & \Rightarrow f\left( x \right)={{x}^{2}}-3x-x+3 \\
 & \Rightarrow f\left( x \right)=x\left( x-3 \right)-1\left( x-3 \right) \\
 & \Rightarrow f\left( x \right)=\left( x-1 \right)\left( x-3 \right) \\
\end{align}\]
Substituting \[f\left( x \right)=0\] and finding the values of x, we have,
\[\Rightarrow x=1\] and x = 3
Representing these values on the number line along with the lower limit 0 and upper limit 4 of the given integral, we have,

Since, we have to find the integral from 0 to 4 so the values of x in the interval \[\left( -\infty ,0 \right)\] and \[\left( 4,\infty \right)\] can be neglected. Now, checking the sign of function \[f\left( x \right)\] in the three intervals (0, 1); (1, 3) and (3, 4), we have,

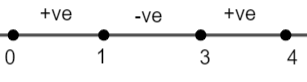
So, the given integral ‘I’ can be broken as: -
\[\begin{align}
  & \Rightarrow I=\int\limits_{0}^{1}{\left( {{x}^{2}}-4x+3 \right)dx}+\int\limits_{1}^{3}{-\left( {{x}^{2}}-4x+3 \right)dx}+\int\limits_{3}^{4}{\left( {{x}^{2}}-4x+3 \right)dx} \\
 & \Rightarrow I=\left[ \dfrac{{{x}^{3}}}{3}-\dfrac{4{{x}^{2}}}{2}+3x \right]_{0}^{1}-\left[ \dfrac{{{x}^{3}}}{3}-\dfrac{4{{x}^{2}}}{2}+3x \right]_{1}^{3}+\left[ \dfrac{{{x}^{3}}}{3}-\dfrac{4{{x}^{2}}}{2}+3x \right]_{3}^{4} \\
\end{align}\]
Substituting the values of limits and simplifying, we get,
\[\Rightarrow I=\left[ \left( \dfrac{1}{3}-2+3 \right)-\left( 0 \right) \right]-\left[ \left( 9-18+9 \right)-\left( \dfrac{1}{3}-2+3 \right) \right]+\left[ \left( \dfrac{64}{3}-32+12 \right)-\left( 9-18+9 \right) \right]\]
\[\Rightarrow I=\] 4 square units.
Hence, the value of the integral is 4 square units.

Note: One may note that without removing the modulus sign we cannot find the integral value because we don’t know the sign of the function in certain intervals. Remember the basic approach that we have used to solve the question. The purpose of representing the values of x and the limits on the number line was to visualize the situation in a better way. Remember that the integration of a function denotes the area under the curve and the unit of area is square units, so it must be mentioned in the end.