
Evaluate using long division method:
$\sqrt{7056}$
Answer
610.5k+ views
Hint: Follow the rule of division method for finding the square root of any number. Put bars from the unit place and use two digits for one bar. Now think of the largest number whose square is even to just less than the first bar digit in the number. Now subtract and bring down the quotient to the divisor, now add a new digit in quotient and divisor (in front) and repeat it to get the quotient. At last when the remainder becomes 0, quotient is the square root of it.
Complete step-by-step answer:
Division method for finding square root can be given as
(a) First place a bar over every pair of digits starting from unit digit, if the number of digits are odd then the left most single digit will also have a bar.
(b) Think of the largest number whose square is even to first less than the first bar digit. Take this number as divisor and also as quotient.
(c) Next subtract the product of the divisor and the quotient from the first bar digit and bring down the next pair of digits which have a bar to the right side of the remainder, that becomes a new dividend.
(d) Now, the new divisor is obtained by adding the first divisor and the quotient and add a digit to the right side of it that we have to choose according to the new dividend which is chosen in such a way that product of new divisor and this digit is less than or equal to the new dividend.
(e) Repeat steps (b, c, d) till the bar digit has been taken up. Now quotient is the required square root of the given number.
Now, let us find out the square root of 7056. Now, putting the bars on digits from behind we can represent the number as
$=\overline{70}\overline{56}$
Now, by the first step try to think of a number whose square is just less than 70.
${{8}^{2}}<70<{{9}^{2}}$
So, put 8 in divisor and quotient both we get,

Now, add the quotient digit to the divisor we get,
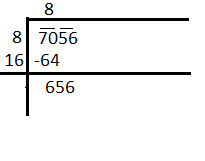
Now, we need to put the same number 16 (in divisor) and in the quotient such that multiplication of divisor formed after putting the digit and the same digit in the quotient as well. So we get

Hence, the square root of 7056 is 84 as remainder becomes 0.
Note: Check the square root by prime factorization as well by making a group of two same numbers.
$\begin{align}
& 2\left| \!{\underline {\,
7056 \,}} \right. \\
& 2\left| \!{\underline {\,
3528 \,}} \right. \\
& 2\left| \!{\underline {\,
1764 \,}} \right. \\
& 2\left| \!{\underline {\,
882 \,}} \right. \\
& 3\left| \!{\underline {\,
441 \,}} \right. \\
& 3\left| \!{\underline {\,
147 \,}} \right. \\
& 7\left| \!{\underline {\,
49 \,}} \right. \\
& 7\left| \!{\underline {\,
7 \,}} \right. \\
& \text{ }\left| \!{\underline {\,
1 \,}} \right. \\
\end{align}$
$\begin{align}
& 7056=\overline{2\times 2}\times \overline{2\times 2}\times \overline{3\times 3}\times \overline{7\times 7} \\
& \text{Square root}=2\times 2\times 3\times 7=84 \\
\end{align}$
Square root by long division method will help in cases where finding factors of a given number is difficult. Example:
$\sqrt{539}=73$
Don’t put bars from the starting of a number in the division method. It is a general mistake done by students with this method. Always put the same digit in divisor and quotient. They should be the same for getting the square root. Bars should be only on maximum two digits and minimum on one digit.
Complete step-by-step answer:
Division method for finding square root can be given as
(a) First place a bar over every pair of digits starting from unit digit, if the number of digits are odd then the left most single digit will also have a bar.
(b) Think of the largest number whose square is even to first less than the first bar digit. Take this number as divisor and also as quotient.
(c) Next subtract the product of the divisor and the quotient from the first bar digit and bring down the next pair of digits which have a bar to the right side of the remainder, that becomes a new dividend.
(d) Now, the new divisor is obtained by adding the first divisor and the quotient and add a digit to the right side of it that we have to choose according to the new dividend which is chosen in such a way that product of new divisor and this digit is less than or equal to the new dividend.
(e) Repeat steps (b, c, d) till the bar digit has been taken up. Now quotient is the required square root of the given number.
Now, let us find out the square root of 7056. Now, putting the bars on digits from behind we can represent the number as
$=\overline{70}\overline{56}$
Now, by the first step try to think of a number whose square is just less than 70.
${{8}^{2}}<70<{{9}^{2}}$
So, put 8 in divisor and quotient both we get,

Now, add the quotient digit to the divisor we get,
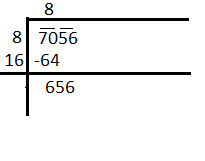
Now, we need to put the same number 16 (in divisor) and in the quotient such that multiplication of divisor formed after putting the digit and the same digit in the quotient as well. So we get

Hence, the square root of 7056 is 84 as remainder becomes 0.
Note: Check the square root by prime factorization as well by making a group of two same numbers.
$\begin{align}
& 2\left| \!{\underline {\,
7056 \,}} \right. \\
& 2\left| \!{\underline {\,
3528 \,}} \right. \\
& 2\left| \!{\underline {\,
1764 \,}} \right. \\
& 2\left| \!{\underline {\,
882 \,}} \right. \\
& 3\left| \!{\underline {\,
441 \,}} \right. \\
& 3\left| \!{\underline {\,
147 \,}} \right. \\
& 7\left| \!{\underline {\,
49 \,}} \right. \\
& 7\left| \!{\underline {\,
7 \,}} \right. \\
& \text{ }\left| \!{\underline {\,
1 \,}} \right. \\
\end{align}$
$\begin{align}
& 7056=\overline{2\times 2}\times \overline{2\times 2}\times \overline{3\times 3}\times \overline{7\times 7} \\
& \text{Square root}=2\times 2\times 3\times 7=84 \\
\end{align}$
Square root by long division method will help in cases where finding factors of a given number is difficult. Example:
$\sqrt{539}=73$
Don’t put bars from the starting of a number in the division method. It is a general mistake done by students with this method. Always put the same digit in divisor and quotient. They should be the same for getting the square root. Bars should be only on maximum two digits and minimum on one digit.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




