Question

What is an example of a real world situation that implies the perpendicular bisector theorem?

Answer 1

Hint: For solving this question you should know about the perpendicular bisector theorem. According to the definition of perpendicular bisector theorem, if a line divides another line segment into two equal halves, through its midpoint at ${{90}^{\circ }}$, it is known as the perpendicular bisector of that line segment. And the theorem states that any point on the perpendicular bisector is equal from the end points of the line segment.

Complete step-by-step solution:
According to our question we have to give an example of a real application of perpendicular bisector theorem. As we know that if any lines divide the other line into two equal halves or at the midpoint of that line at an angle of ${{90}^{\circ }}$, then it is known as the perpendicular bisector of that line segment. And the perpendicular bisector theorem states that all the points at the perpendicular line are always equal to both end points of this line.

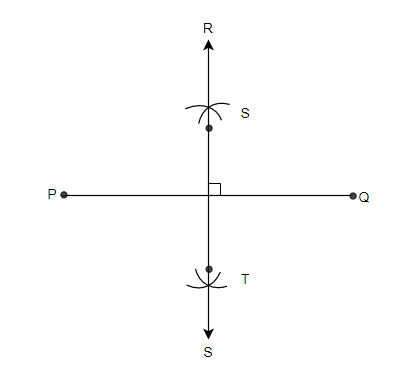
Perpendicular bisector theorem

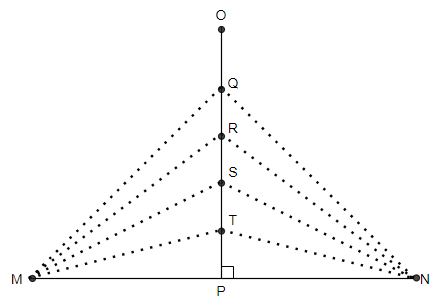
In this figure
MT = NT
MS = NS
MR = NR
MQ = NQ
If we see the real life example of perpendicular bisector theorem, then we can see the volleyball net at any beach. The figure of that would be like this:

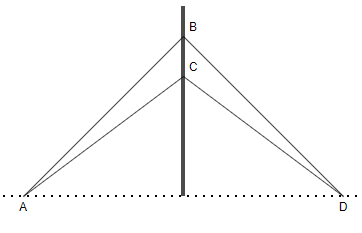
So, according to the diagram it is clear that the pole of the volleyball at the beach is standing with the help of ropes AB = AC and BD = CD. And by measuring we can see that AC and CD and AB and BD have equal lengths, which implies the perpendicular bisector theorem.
So, the example for a perpendicular bisector theorem is a volleyball net’s pole at the beach.

Note: If we see the diagram of perpendicular bisector theorem, then it is clear that we can also calculate the length of the pole if this is not given. And if the question asks to calculate the length of the arms, then all of these can be calculated by Pythagoras theorem which is ${{x}^{2}}={{y}^{2}}+{{z}^{2}}$.