Question

What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20°C) is\[2.50 \times {10^{ - 2}}N{m^{ - 1}}\]? If an air bubble of the same dimension were formed at a depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is \[1.01 \times {10^5}\] Pa)

Answer 1

Hint: Before attempting the question, prior knowledge of the relation between pressure and surface tension is must according to which $P = \dfrac{{2S}}{r}$here S is the surface tension acting on the surface of the air bubble and r is the radius of the bubble, use this information to approach towards the solution.

Complete step-by-step solution:
According to the given question we have a soap bubble of radius 5 mm with surface tension \[2.50 \times {10^{ - 2}}N{m^{ - 1}}\] at 20°C and for case 2 we got an air bubble of the same radius and surface tension as a soap bubble which is in the depth of 40 cm in a soap solution containing container which has a relative density of 1.20
Since the relative density of soap solution is 1.20
So we can say that the density of soap solution is $1.2 \times {10^3}kg/{m^3}$
For case 1:

We have radius of soup bubble = 5.00 mm = \[5 \times {10^{ - 3}}\] m
Surface tension at temp (20°C) of soup bubble is, S = \[2.50 \times {10^{ - 2}}N{m^{ - 1}}\]
So by the relation between excess pressure inside the bubble and surface tension acting on it is given by $P = \dfrac{{2S}}{r}$
Since in the case of soup bubble we have 2 surfaces – inside and out therefore the relation between excess pressure inside the soap bubble and surface tension is given by $P = \dfrac{{4S}}{r}$
Substituting the given values in the above equation
We get $P = \dfrac{{4 \times 2.5 \times {{10}^{ - 2}}}}{{5 \times {{10}^{ - 3}}}}$
$ \Rightarrow $$P = \dfrac{{100}}{5}$
$ \Rightarrow $$P = 20$Pa
Therefore the maximum pressure experienced by the soup bubble will be 20 Pa
For case 2 we have

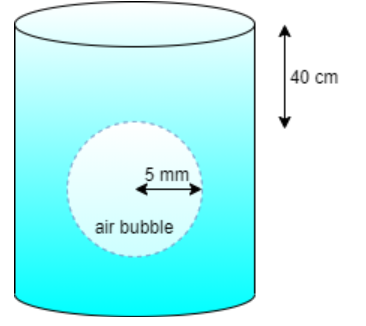
Radius of air bubble = 5.00 mm = \[5 \times {10^{ - 3}}\] m
Depth of air bubble i.e. h = 40 cm = 0.4 m
Surface tension of air bubble is, S = \[2.50 \times {10^{ - 2}}N{m^{ - 1}}\]
Density of soap solution = $1.2 \times {10^3}kg/{m^3}$
1 atmospheric pressure is given = $1.01 \times {10^5}Pa$
Given acceleration due to gravity = 9.8 m/${s^2}$
By the relation between excess pressure inside air bubble and surface tension we can say that $P' = \dfrac{{2S}}{r}$
Substituting the given values in the above equation
We get, $P' = \dfrac{{2 \times 2.50 \times {{10}^{ - 2}}}}{{5 \times {{10}^{ - 3}}}}$
$ \Rightarrow $$P' = \dfrac{{50}}{5}$
$ \Rightarrow $$P' = 10$Pa
So the excess pressure inside the bubble made of air is equal to 10 Pa
Since we know that in this case inside the solution of soup the bubble will experience pressure due to soap solution, atmospheric pressure and pressure inside the air bubble
Therefore total pressure inside the bubble made of air is given by ${P_t} = {P_a} + {P_o} + P'$ here $P_t$ is atmospheric pressure, $P_a$ is atmospheric pressure, $P_o$ is pressure exerted by liquid on bubble and P’ represents the excess pressure inside the air bubble where pressure due to liquid ($P_o$) is given by$\rho gh$, atmospheric pressure is given $1.01 \times {10^5}Pa$ and excess pressure inside the bubble is given by $P' = \dfrac{{2S}}{r}$
Taking equation ${P_t} = {P_a} + \rho gh + P'$ as equation 1
Substituting the given values in the equation 1
We get ${P_t} = 1.01 \times {10^5} + (1.2 \times {10^3} \times 9.8 \times 0.4) + 10$
$ \Rightarrow $${P_t} = 1.057 \times {10^5}$ Pa $ \approx $ $1.06 \times {10^5}$ Pa
Hence the total pressure inside the bubble will be $1.06 \times {10^5}$ Pa

Note: The term surface tension that we came across in the above solution can be explained as the characteristics of a liquid which oppose the effect of force that is applied externally, the cohesive nature of liquid is the reason behind the resisting nature of liquid towards the external forces applied. For example, when a bottle is kept on the surface of liquid it keeps floating on the surface this happens because of the cohesive nature of the liquid.