
What is the excess pressure inside a soap bubble with a radius of 1.5 cm and the surface tension of 0.03 N/m?
A.7 pa
B.3 pa
C.2 pa
D.8 pa
Answer
430.6k+ views
Hint: In this question we first write all the force component that are acting on the bubble and then equate them following the sign convention that is
Complete step-by-step answer:
First will find the excess pressure for a spherical bubble in water and for that, we first draw the cross-section view of a spherical bubble with radius R equal to 1.5 cm and surface tension T equal to 0.03 N/m as can be shown in figure 1.
We know that a bubble has two liquid surfaces in contact with air, one is the inner surface of the bubble and the other one is the outer surface of the bubble. So, the force due to surface tension will become
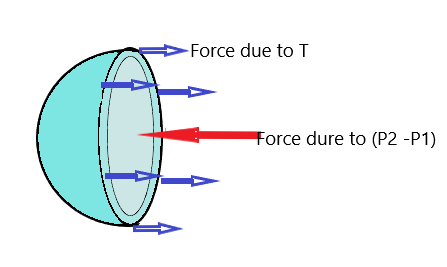
Figure 1
Now writing the all forces acting on the bubble that are
Force due to the external pressure that is
Force due to the internal pressure that is
Force due to the surface tension that is
Since the drop is in equilibrium we will get
Now substituting
Hence the Excess pressure
So option D is correct.
Note:For these types of questions, we need the concept of surface tension and pressure due to the air-water interface. We also need to remember the excess pressure for different shapes of the air-water interface that we see in real life that is cylindrical drops and bubbles, spherical drops and bubbles, and meniscus. We need to know how excess pressure varies with the free surfaces and how to calculate numerically related to this topic.
Complete step-by-step answer:
First will find the excess pressure for a spherical bubble in water and for that, we first draw the cross-section view of a spherical bubble with radius R equal to 1.5 cm and surface tension T equal to 0.03 N/m as can be shown in figure 1.
We know that a bubble has two liquid surfaces in contact with air, one is the inner surface of the bubble and the other one is the outer surface of the bubble. So, the force due to surface tension will become

Figure 1
Now writing the all forces acting on the bubble that are
Force due to the external pressure that is
Force due to the internal pressure that is
Force due to the surface tension that is
Since the drop is in equilibrium we will get
Now substituting
Hence the Excess pressure
So option D is correct.
Note:For these types of questions, we need the concept of surface tension and pressure due to the air-water interface. We also need to remember the excess pressure for different shapes of the air-water interface that we see in real life that is cylindrical drops and bubbles, spherical drops and bubbles, and meniscus. We need to know how excess pressure varies with the free surfaces and how to calculate numerically related to this topic.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

In northern hemisphere 21st March is called as A Vernal class 11 social science CBSE




