Question

Explain Lorentz-Fitzgerald contraction with an example.

Answer 1

Hint: To get the in-depth idea about Lorentz-Fitzgerald contraction first of all we have to understand the basic two postulates of the special theory of relativity. All the derivation on this topic is revolving around these two considerations:-
1. The principle of relativity- All the laws of physics have the same form in all inertial frames of references.
2. The constancy of the speed of light – the speed of light is the maximum speed having a constant value of about \[3 \times {10^8}m/s\]. The speed of light is the same for all observers whether they are in rest or motion.

Complete step by step answer:
Lorentz-Fitzgerald contraction:-
H.A. Lorentz and G.F. Fitzgerald proposed that when an object moves with very high speed the length of the object gets contracted in the direction of its motion. This length-contraction event was given a theoretical background in Einstein’s special theory of relativity. To get a more in-depth understanding of this topic We consider a rod at rest in frame S’ whose two ends have coordinates 0 and L. In this frame, the length of the in S’ frame will be \[L - 0 = L\].

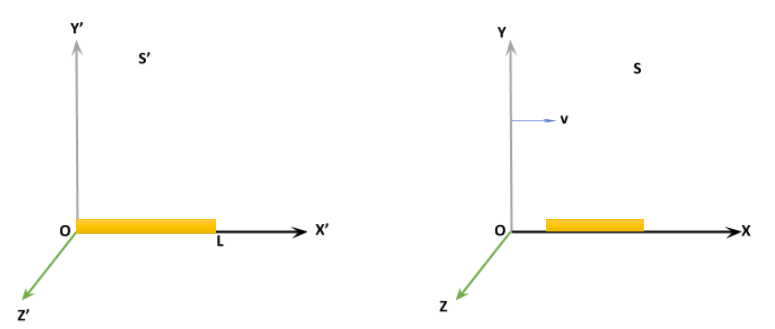
We consider another frame S which is moving with velocity v along x-direction with respect to S’ frame.
Let \[{x_1}\] and \[{x_2}\]are the x-coordinates of the rod ends such that: \[({x_2} - {x_1}) = L'\].
Now we measure the length of the rod in the S frame and we find the difference of two coordinates of the rod ends at the instant of time. This results in the length contraction of the rod in the $S$ frame.
Mathematical Expressions:
According to Lorentz transformation -
\[x' = \gamma (x - vt)\], where \[\gamma = \sqrt {1 - \dfrac{{{v^2}}}{{{c^2}}}} \]
Applying Lorentz transformation in S’ frame, we get
\[0 = \gamma ({x_1} - vt)\]………… (i)
\[L = \gamma ({x_2} - vt)\]……….. (ii) (where \[{x_2}\]and \[{x_1}\]are the x-coordinates of the ends of the rod in S’ frame)
Subtracting (ii) from (i)
\[L = \gamma ({x_2} - {x_1})\]
\[ \Rightarrow ({x_2} - {x_1}) = \dfrac{L}{\gamma }\]………. (iii)
Since we assume that \[({x_2} - {x_1}) = L'\]
Therefore equation (iii) becomes-
\[L' = \dfrac{L}{\gamma }\] ……….. (iv)
 Substitute the value of \[\gamma = \sqrt {1 - \dfrac{{{v^2}}}{{{c^2}}}} \] in equation (iv), we get
 \[L' = L\sqrt {1 - \dfrac{{{v^2}}}{{{c^2}}}} \]
As \[\sqrt {1 - \dfrac{{{v^2}}}{{{c^2}}}} < 1\]

$\therefore $ \[L' < L\], which indicates that a moving rod is shortened. This is also called Lorentz -Contraction.

Note:
H.A Lorentz and G.F Fitzgerald were two super brains (Theoretical Physicists) who had independently proposed the hypothesis of length contraction in the special theory of relativity. The hypothesis of length contraction firstly came into lame light when it reformed the Galilean invariance hypothesis and built a milestone for the expansion of the Einstein theory of relativity. Students must read this chapter from the historical background of relativity. It will definitely expand the thinking ability of the students.