
Explain the formation of standing waves in case of an organ pipe open at one end and closed at the other end. Represent the first three modes of vibration diagrammatically and find their frequencies.
Answer
232.8k+ views
Hint: In this solution, we will use the relation of sound wave speed, distance, and velocity to determine the formation of standing waves and their frequencies. In a closed pipe, there is an antinode at the open end and a node at the closed end.
Complete step by step answer:
When sound waves are incident in a closed tube, they travel in the form of longitudinal waves. The waves that reach the closed bottom end of the tube, they are reflected back as shown in the diagrams below.
The closed wall of the tube acts as a rigid wall. This is because the air at the closed end is not free to vibrate. So, the reflected wave and the incident interfere with each other and form standing waves inside the organ. In this situation, a node is formed at the closed end. The air at the open end is free to vibrate with maximum amplitude and hence an antinode is formed there. This is the simplest mode of vibration of an air column in a closed well and is called the fundamental mode
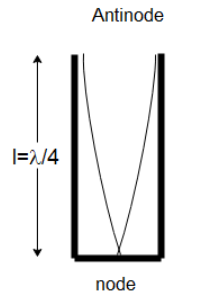
We know that the velocity of a sound wave is the product of its frequency and wavelength i.e.
$v = f.\lambda $
In the standing mode, the wavelength of the wave must be such that
$n\lambda = 4L$ where $n$ is the order of the harmonic. For the fundamental harmonic, $n = 1$. And $L$ is the length of the pipe.
Using the above two relations, we can write
$\dfrac{{nv}}{f} = 4L$
$ \Rightarrow f = \dfrac{v}{{4L}}\,{\text{(for n = 1)}}$
Now for a closed pipe, only antinodes can be formed at the open end of the pipe to form standing waves. So, only odd values of $n$ will be allowed to create standing waves as shown in the diagrams below.
So, the second overtone and the third overtone will have frequencies
${f_2} = \dfrac{{3v}}{{4l}}$
And
${f_3} = \dfrac{{5v}}{{4l}}$
The diagrams of the second and the third overtone respectively are shown below:
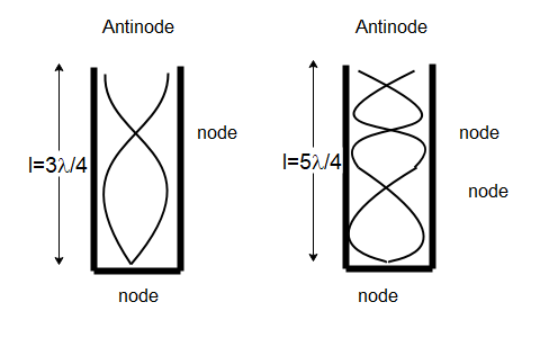
Note: While calculating the frequencies of the harmonic overtones, we must be careful that we select only odd values of \[n\]. This is because, for even values of $n$, an antinode will not be formed at the open end and standing waves won’t be able to form.
Complete step by step answer:
When sound waves are incident in a closed tube, they travel in the form of longitudinal waves. The waves that reach the closed bottom end of the tube, they are reflected back as shown in the diagrams below.
The closed wall of the tube acts as a rigid wall. This is because the air at the closed end is not free to vibrate. So, the reflected wave and the incident interfere with each other and form standing waves inside the organ. In this situation, a node is formed at the closed end. The air at the open end is free to vibrate with maximum amplitude and hence an antinode is formed there. This is the simplest mode of vibration of an air column in a closed well and is called the fundamental mode

We know that the velocity of a sound wave is the product of its frequency and wavelength i.e.
$v = f.\lambda $
In the standing mode, the wavelength of the wave must be such that
$n\lambda = 4L$ where $n$ is the order of the harmonic. For the fundamental harmonic, $n = 1$. And $L$ is the length of the pipe.
Using the above two relations, we can write
$\dfrac{{nv}}{f} = 4L$
$ \Rightarrow f = \dfrac{v}{{4L}}\,{\text{(for n = 1)}}$
Now for a closed pipe, only antinodes can be formed at the open end of the pipe to form standing waves. So, only odd values of $n$ will be allowed to create standing waves as shown in the diagrams below.
So, the second overtone and the third overtone will have frequencies
${f_2} = \dfrac{{3v}}{{4l}}$
And
${f_3} = \dfrac{{5v}}{{4l}}$
The diagrams of the second and the third overtone respectively are shown below:

Note: While calculating the frequencies of the harmonic overtones, we must be careful that we select only odd values of \[n\]. This is because, for even values of $n$, an antinode will not be formed at the open end and standing waves won’t be able to form.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




