
Explain why square is also a parallelogram ?
Answer
528k+ views
Hint: A square has all the properties of a parallelogram and also has some additional properties. So, let us draw a square ABCD and state all its properties.
Complete step-by-step answer:
As we know that the properties of a parallelogram can be stated according to the sides, the angles, the diagonals and the symmetry.
So, the properties of parallelogram are,
It has 2 pairs of opposite sides parallel.
It has 2 pairs of opposite sides equal.
The sum of the angles of a parallelogram is equal to
2 pairs of opposite angles of a parallelogram are equal.
The diagonals of a parallelogram bisect each other.
A parallelogram has 2 lines of symmetry.
Now as we know that all of the above stated properties also apply to squares. So, it can be considered to be a parallelogram. However, a square has additional properties as well, so it can be regarded as a special type of parallelogram.
A square has :
2 pairs of opposite sides parallel
All its sides equal.
The sum of the angles of a square is equal to
All the angles of a square are equal to
The diagonals of a square bisect each other at
A square has 4 lines of symmetry.
So, now we can see from the above properties of the square that all the properties of a parallelogram also apply to the square.
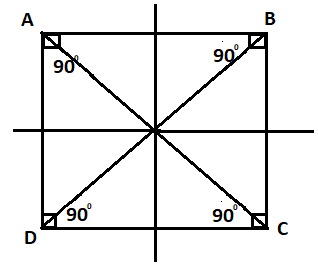
So, that’s why parallelograms are also square.
Note: Whenever we come up with this type of problem then we should remember that the squares, rectangles and rhombus are the special type of parallelogram because all the properties of a parallelogram also apply to the square, rectangle and rhombus however they have some additional properties which parallelogram does not have. So, all parallelograms are not square, rectangles and rhombus.
Complete step-by-step answer:
As we know that the properties of a parallelogram can be stated according to the sides, the angles, the diagonals and the symmetry.
So, the properties of parallelogram are,
It has 2 pairs of opposite sides parallel.
It has 2 pairs of opposite sides equal.
The sum of the angles of a parallelogram is equal to
2 pairs of opposite angles of a parallelogram are equal.
The diagonals of a parallelogram bisect each other.
A parallelogram has 2 lines of symmetry.
Now as we know that all of the above stated properties also apply to squares. So, it can be considered to be a parallelogram. However, a square has additional properties as well, so it can be regarded as a special type of parallelogram.
A square has :
2 pairs of opposite sides parallel
All its sides equal.
The sum of the angles of a square is equal to
All the angles of a square are equal to
The diagonals of a square bisect each other at
A square has 4 lines of symmetry.
So, now we can see from the above properties of the square that all the properties of a parallelogram also apply to the square.

So, that’s why parallelograms are also square.
Note: Whenever we come up with this type of problem then we should remember that the squares, rectangles and rhombus are the special type of parallelogram because all the properties of a parallelogram also apply to the square, rectangle and rhombus however they have some additional properties which parallelogram does not have. So, all parallelograms are not square, rectangles and rhombus.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Whom did king Ashoka send to Sri Lanka to spread Buddhism class 7 social science CBSE

The southernmost point of the Indian mainland is known class 7 social studies CBSE

How many crores make 10 million class 7 maths CBSE

AIM To prepare stained temporary mount of onion peel class 7 biology CBSE

Find HCF and LCM of 120 and 144 by using Fundamental class 7 maths CBSE





