Question

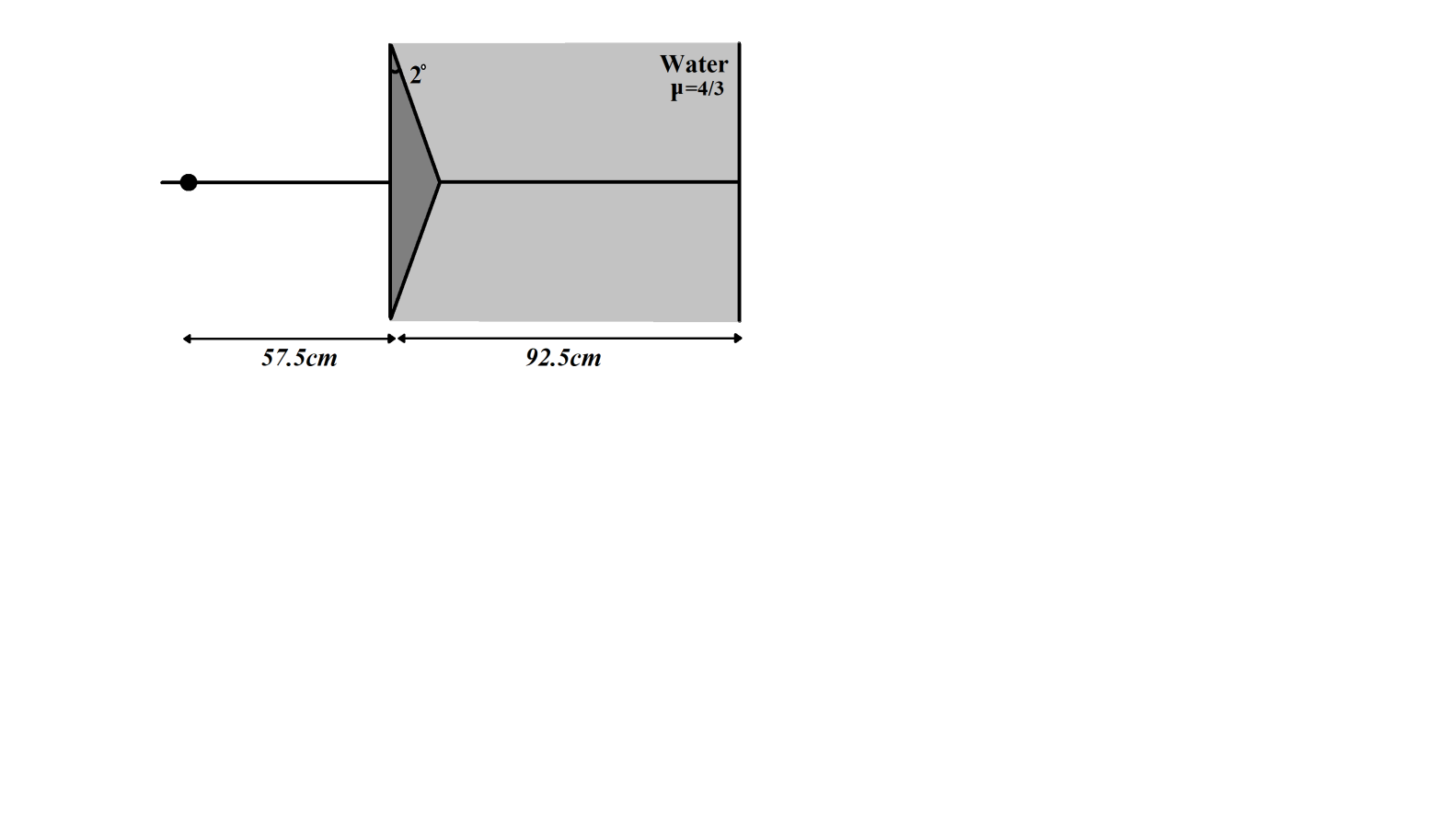
Figure shows a modified Fresnel biprism experiment with monochromatic source of wavelength$500nm$. The refracting angle of the prism is${{2}^{\circ }}$. Find the fringe width.

$\begin{align}
  & \text{A}\text{. }0.1125mm \\
 & \text{B}\text{. }0.125mm \\
 & \text{C}\text{. }0.15mm \\
 & \text{D}\text{. }0.3mm \\
\end{align}$

Answer 1

Hint: When a monochromatic light source is kept in front of biprism, two coherent virtual sources are produced. Fringe width is described as the distance between two consecutive dark fringes or two consecutive bright fringes obtained on the screen. We will use the expression for fringe width relating the wavelength of incident light, distance between the coherent sources and distance between the source and the screen.
Formula used:
Fringe width, $\beta =\dfrac{\lambda D}{d}$
Angle of deviation of prism with water on one side is, $\delta =A\left( {{\mu }_{g}}-\mu \right)$
Distance between the sources, $d=2\delta l$

Complete step by step solution:
Fresnel biprism is an optical device for producing interference of light waves. It can be formed by joining base to base two thin prisms of very small refracting angles.
When a monochromatic light source is kept in front of biprism, two coherent virtual sources are produced. Interference fringes are obtained on the screen placed behind the prism. Interference pattern is observed on a limited region of the screen.
Fringe width is described as the distance between two consecutive dark fringes or two consecutive bright fringes obtained on the screen.
Fringe width is given as,
$\beta =\dfrac{\lambda D}{d}$
Where,
$\beta $is the fringe width
$D$is the distance between the slit and screen
$d$is the distance between the sources
We are given a Fresnel biprism having refracting angle${{2}^{\circ }}$. Monochromatic source has wavelength$500nm$.

Refractive index of glass, ${{\mu }_{g}}=1.5$
Angle of deviation of prism with water on one side is,
$\delta =A\left( {{\mu }_{g}}-\mu \right)$
Where,
$A$is the angle of prism
${{\mu }_{g}}$is the refractive angle of glass
$\mu $is the refractive index of water
Putting values of$A,\text{ }{{\mu }_{g}}$and ${{\mu }_{m}}$
$\begin{align}
  & A=\dfrac{2}{180} \\
 & {{\mu }_{g}}=\dfrac{3}{2} \\
 & {{\mu }_{m}}=\dfrac{4}{3} \\
\end{align}$
$\begin{align}
  & \delta =\dfrac{2}{180}\times \dfrac{22}{7}\left( \dfrac{3}{2}-\dfrac{4}{3} \right) \\
 & \delta =\dfrac{2}{180}\times \dfrac{22}{7}\times \dfrac{1}{6} \\
 & \delta =\dfrac{11}{90\times 7\times 3} \\
\end{align}$
Now,
$d=2\delta l$
Where,
$d$ is the distance between the sources
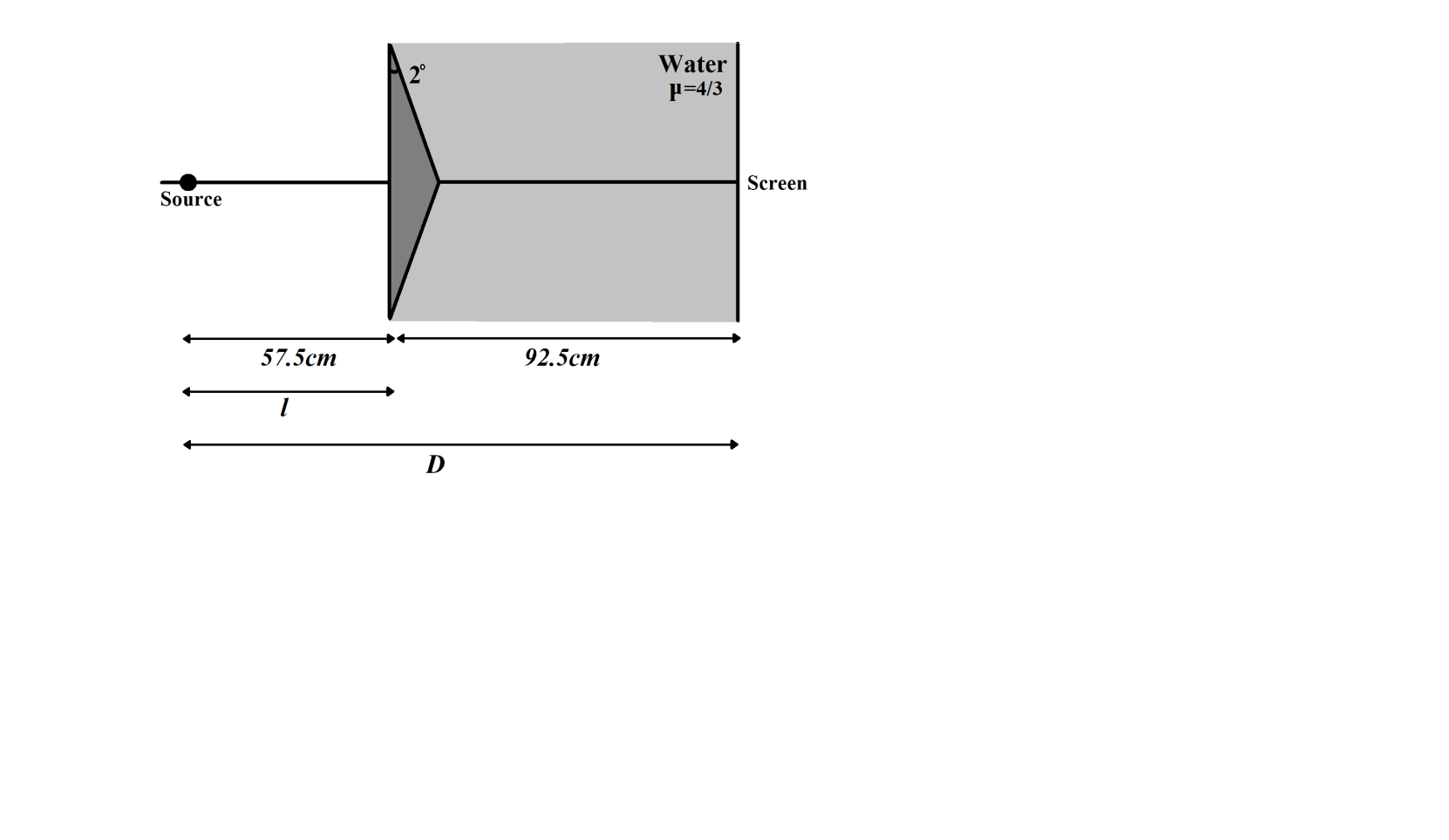
$l$is the distance between source and fresnel prism
Putting values of $\delta $and $l$
$\begin{align}
  & \delta =\dfrac{11}{90\times 7\times 3} \\
 & l=57.5cm=0.575m \\
\end{align}$
$\begin{align}
  & d=2\times \left( \dfrac{11}{90\times 3\times 7} \right)\times 0.575 \\
 & d=\dfrac{11\times 1.15}{90\times 3\times 7} \\
 & d=\dfrac{11\times 0.23}{18\times 3\times 7} \\
\end{align}$
Now,
Fringe width is given as,
$\beta =\dfrac{\lambda D}{d}$
Where,
$\beta $is the fringe width
$\lambda $is the wavelength of incident light
$D$is the distance between the sources and the screen
$d$ is the distance between the sources
Putting values,
\[\begin{align}
  & \lambda =500nm=500\times {{10}^{-9}}m \\
 & D=\left( 57.5+92.5 \right)cm=150cm=1.5m \\
 & d=\dfrac{11\times 0.23}{18\times 3\times 7}m \\
\end{align}\]
\[\begin{align}
  & \beta =\dfrac{500\times {{10}^{-9}}\times 1.5}{\dfrac{11\times 0.23}{18\times 3\times 7}} \\
 & \beta =\dfrac{500\times {{10}^{-9}}\times 1.5\times 18\times 3\times 7}{11\times 0.23} \\
 & \beta =0.1125mm \\
\end{align}\]
The fringe width of the given experimental set up is $0.1125mm$
Hence, the correct option is B.

Note:
Fringe width is the distance between two consecutive dark fringes or two consecutive bright fringes. In case of a hollow prism or fluid prism, relative refractive index has to be considered, in place of absolute refractive index, while calculating angle of deviation of the prism.