Question

Figure shows a planet in an elliptical orbit around the Sun S. Where is the kinetic energy of the planet maximum?

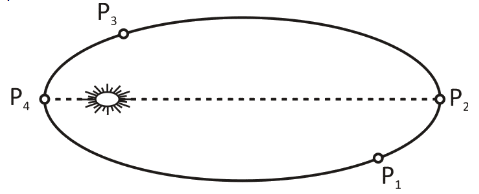
A. ${P_1}$
B. ${P_2}$
C. ${P_3}$
D. ${P_4}$

Answer 1

Hint:Here we have to apply the concept of angular momentum and kinetic energy.In mechanics, angular momentum is the rotational counterpart to linear momentum (rarely, momentum or rotational momentum). In mechanics, it is an important quantity since it is a conserved quantity; a closed system's cumulative angular momentum stays unchanged. In physics, an object's kinetic energy (KE) is the energy it possesses because of its motion. It is defined as the work required in accelerating from rest to the specified velocity of a body of a given mass.

Complete step by step answer:
The angular momentum of rigid bodies is preserved; a rotating object can thus continue to rotate until an outside force acts on it. Angular momentum shifts are torque-equivalent.
Angular momentum is given by:
$L = mvr$
Where $m$ is the mass, $v$ is the velocity and $r$ is the radius.

Angular momentum is conserved, including energy and linear momentum. Another symbol of inherent unity of physical laws is this generally applicable statute. When the net external torque is zero, angular momentum is maintained, just as linear momentum is retained when the net external force is zero. For the angular momentum to be constant, $mvr$ should be equal to constant.
Thus $mvr = {\text{constant}}$
Thus, $v\alpha \dfrac{1}{r}$
So, when the velocity is maximum, radius is minimum as velocity is inversely proportional to the radius. Radius $r$ is minimum at the point ${P_4}$. Here velocity is maximum.
So, kinetic energy, $K.E = \dfrac{1}{2}m{v^2}$
Since, kinetic energy is directly proportional to the velocity. So, kinetic energy is maximum at the point ${P_4}$.

Hence, option D is correct.

Note:Here we have to see that diagram which point is further away from the sun. Otherwise if we write points, then the answer would be wrong. As long as their sum stays continuous, any of the individual angular moments can alter. When the external force on a structure is zero, this law is equivalent to linear momentum being maintained.