Question

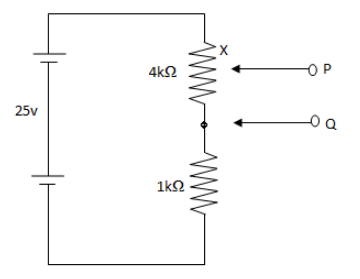
Figure shows a potential divider circuit, which by adjustment of the position of the contact X, can be used to provide a variable potential difference between the terminals P and Q. What are the limits of this potential difference?

A. \[0\] and \[20\,{\text{mV}}\]
B. \[{\text{5}}\] and \[25\,{\text{mV}}\]
C. \[0\] and \[20\,{\text{V}}\]
D. \[0\] and \[25\,{\text{V}}\]

Answer 1

Hint: We are asked to find the lower limit and upper limit of potential difference between the terminals P and Q. To find the lower limit move the terminal P to the lower end of resistor \[{\text{4}}\,{\text{k}}\Omega \] and to find the upper limit, move the terminal P to the upper end of resistor \[{\text{4}}\,{\text{k}}\Omega \].

Complete step by step answer:
We are given a circuit and asked to find the range of potential difference between the terminals P and Q.Let us first find the lower limit of the potential difference between the terminals P and Q.We can find the lower limit of potential difference by moving the terminal P to the lower end of \[{\text{4}}\,{\text{k}}\Omega \] resistor that is towards terminal Q. In this case, the potential difference between P and Q will be zero. Therefore, the lower limit of the potential difference between the terminals P and Q will be \[0\,{\text{V}}\].

Now, we find the upper limit of potential difference between the terminals P and Q. In this case we move the terminal P to the upper end of \[{\text{4}}\,{\text{k}}\Omega \] resistor that is away from the terminal Q.Here, let \[i\] be the current flowing through the circuit.
We redraw the circuit.

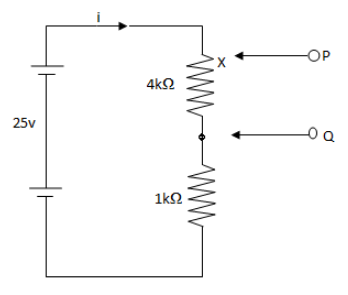
Here, the equivalent resistance will be,
\[R = {\text{4}}\,{\text{k}}\Omega + 1\,{\text{k\Omega }}\]
\[ \Rightarrow R = 5\,{\text{k}}\Omega \]
Current through a circuit is,
\[{\text{voltage}} = {\text{current}} \times {\text{resistance}}\] (i)
Here, voltage is \[25\,{\text{V}}\]
Putting the values of voltage and equivalent resistance in equation (i) we get,
\[25\, = i \times 5\]
\[ \Rightarrow i\, = \dfrac{{25}}{5} = 5\,{\text{A}}\]
Now, voltage across the resistor \[{\text{4}}\,{\text{k}}\Omega \] will be (using equation (i))
\[{V_{PQ}} = i \times 4\]
Putting the value of \[i\] in the above equation we get,
\[{V_{PQ}} = 5 \times 4\]
\[ \therefore {V_{PQ}} = 20\,{\text{V}}\]
Therefore, the upper limit of potential difference between the terminals P and Q is \[20\,{\text{V}}\].So, the limits of potential difference between the terminals P and Q are \[0\,{\text{V}}\]and \[20\,{\text{V}}\].

Hence, the correct answer is option C.

Note:Using a potential divider circuit, we can get different voltages from a common supply voltage. One example of a potential divider is potentiometer. Potential divider circuits can be used for controlling audio volume, for controlling temperature in the freezer.