
Figure shows a torch producing a straight light beam falling on a plane mirror at an angle
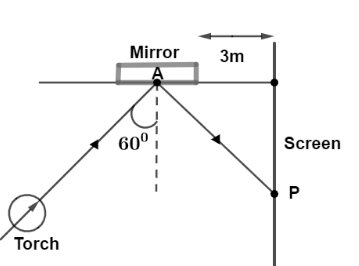
A.
B.
C.
D.

Answer
420.6k+ views
1 likes
Hint: In order to find the speed of spot P, we will find the relation between the distance of spot on y-axis at time
Complete step by step answer:
Let us first draw the diagram when after
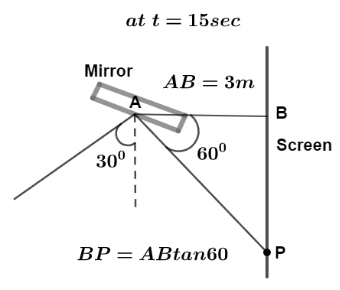
In the right angle triangle
Differentiate above equation with respect to time, we get
So we get,
Now as we know,
Converting
And, from the diagram we have, this
Put all the parameters value in equation
Hence, the correct option is C.
Note:It must be remembered that, the angular speed at which mirror rotates, the reflected ray will rotate by twice the angle with which mirror rotate and hence twice the angular velocity of rotation of reflected ray, and angular velocity of the body is the differentiation of angular displacement with respect to time
Complete step by step answer:
Let us first draw the diagram when after

In the right angle triangle
Differentiate above equation with respect to time, we get
So we get,
Now as we know,
Converting
And, from the diagram we have, this
Put all the parameters value in equation
Hence, the correct option is C.
Note:It must be remembered that, the angular speed at which mirror rotates, the reflected ray will rotate by twice the angle with which mirror rotate and hence twice the angular velocity of rotation of reflected ray, and angular velocity of the body is the differentiation of angular displacement with respect to time
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Why is the cell called the structural and functional class 12 biology CBSE




