Question

How do you find an equation of a parabola given endpoints of the latus rectum are \[(-2,-7)\] and \[(4,-7)\].

Answer 1

Hint: We will start by plotting an appropriate figure parabola of the given endpoints. We have the endpoints of the latus rectum, using these points we can calculate the focus of the parabola using the midpoint formula. Using the point of focus, we can calculate the vertex of the parabola, but since we do not know as in which direction is the parabola open, so we have two equations of parabola for parabola open upwards and downwards as well.

Complete step by step solution:
According to the given question, we have been given the endpoints of the latus rectum and we have to find an equation of the parabola having the latus rectum with the given endpoints.
Firstly, we will plot the given point and draw the possible parabola’s which can be drawn, we have,

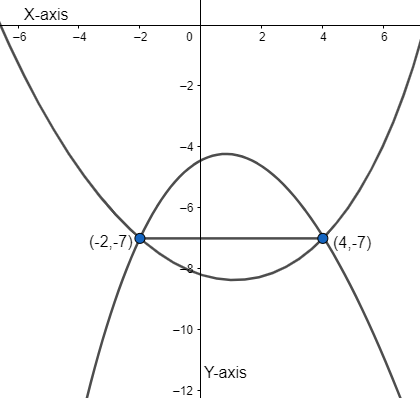
The above plot has two parabolas since we are not given in which the parabola opens. So, using the endpoints given we can get two equations of parabola.
We know that the equation of parabola along the y-axis is \[{{x}^{2}}=4ay\] or \[{{x}^{2}}=-4ay\].
But these equations were valid as the vertex of the parabola was at the origin, but now we cannot use the above equation as the vertex of the parabolas of this question would be a point other than the origin, so we will use the formula:
\[{{(x-h)}^{2}}=4a(y-k)\], when the parabola is open upwards
And \[{{(x-h)}^{2}}=-4a(y-k)\], when the parabola is open downwards
where \[(h,k)\] is the point of vertex of the parabola and \[a\] is the distance from the vertex to the midpoint of the latus rectum.
Latus rectum refers to the line (parallel to the x-axis in the current case) which passes through a focus and its length is 4 times the length from the vertex to the midpoint of the latus rectum.
So as to find the equation of the parabola we have to find the vertex of the parabolas.
We will find the focus of the parabola using the midpoint formula, we have,
\[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
Given endpoints of the latus rectum are: \[(-2,-7)\] and \[(4,-7)\]
We get the focus as,
Focus \[\Rightarrow \left( \dfrac{-2+4}{2},\dfrac{-7+(-7)}{2} \right)\]
\[\Rightarrow \left( \dfrac{2}{2},\dfrac{-14}{2} \right)\]
Focus\[\Rightarrow \left( 1,-7 \right)\]
Now, we have to find the length of the latus rectum using the endpoints of the latus rectum are: \[(-2,-7)\] and \[(4,-7)\], we will use the distance formula.
Distance = \[\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
(As stated above, we know that the length of latus rectum is 4a. Therefore, we have,)
\[4a=\sqrt{{{(4-(-2))}^{2}}+{{(-7-(-7))}^{2}}}\]
\[\Rightarrow 4a=\sqrt{{{(4+2)}^{2}}}\]
\[\Rightarrow 4a=\sqrt{{{6}^{2}}}=\sqrt{36}\]
\[\Rightarrow 4a=6\]
and \[a=\dfrac{6}{4}\]
The value of ‘h’ in the vertex of a parabola has the same value as that of x-coordinate of the focus\[\Rightarrow \left( 1,-7 \right)\],
That is, \[h=1\]
We know that,
\[k=-a-{{y}_{focus}}\], when the parabola is open upwards, we have
\[\Rightarrow k=\dfrac{-6}{4}+(-7)=\dfrac{-34}{4}=\dfrac{-17}{2}\]
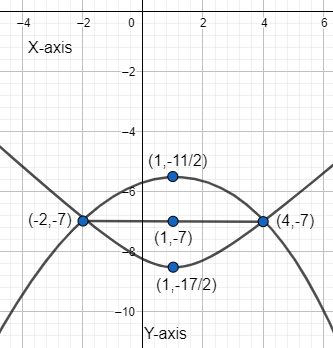
The vertex is \[\left( 1,\dfrac{-17}{2} \right)\]
and
\[k=a+{{y}_{focus}}\], when the parabola is open downwards, we have
\[\Rightarrow k=\dfrac{6}{4}+(-7)=\dfrac{-22}{4}=\dfrac{-11}{2}\]
The vertex is \[\left( 1,\dfrac{-11}{2} \right)\]
Therefore, substituting the values of all the variables we obtained we have,
the equation of the parabola opening upwards and having vertex \[\left( 1,\dfrac{-17}{2} \right)\] is:
\[{{(x-1)}^{2}}=6\left( y-\left( \dfrac{-17}{2} \right) \right)\]
And
the equation of the parabola opening downwards and having vertex \[\left( 1,\dfrac{-11}{2} \right)\] is:
\[{{(x-1)}^{2}}=-6\left( y-\left( \dfrac{-11}{2} \right) \right)\]
So, we have the graph as,

Note:
While solving for the focus of the parabola, the focus should not be intermixed with the vertex of the parabola. Both are two different terms. And the equation for parabola opening upwards and downwards differ only by the presence of a negative sign rest everything is the same. Similarly, the equation to find the value of y component of the vertex varies in sign with parabola facing upwards and downwards.