Question

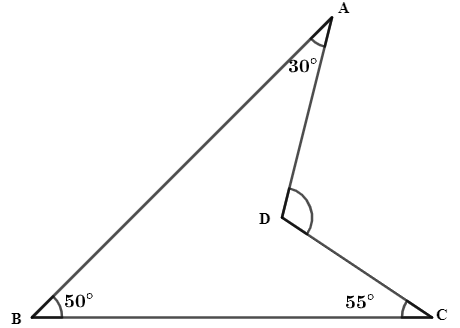
Find $\angle ADC$ from the given figure.

Answer 1

Hint:Find the angle ADC (reflex) which is a reflex angle and forming inside the quadrilateral ABCD. Sum of all the angles of a quadrilateral is \[{{360}^{\circ }}\]. And angle around a point is \[{{360}^{\circ }}\] as well. Calculate the angle ADC as required in the question, using above information.

Complete step-by-step answer:
Given diagram in question is

As we know, the sum of all the interior angles of a quadrilateral is \[{{360}^{\circ }}\]. And we observe that ABCD is also a quadrilateral as it has four sides. So, the sum of all the angles of it will be \[{{360}^{\circ }}\] as well. So, we can write the equation as
\[\angle BAD+\angle ABC+\angle BCD+\angle ADC\] (reflex or inside of quadrilateral) = \[{{360}^{\circ }}\]
So, put the values of angles given in the diagram so, we get
\[30+55+50+\angle ADC\ \left( \text{reflex} \right)\ =\ {{360}^{\circ }}\]
\[135+\angle ADC\ \left( \text{reflex} \right)\ =\ {{360}^{\circ }}\]
\[\angle ADC\ \left( \text{reflex} \right)=\ 360-135\]
\[\angle ADC\ \left( \text{reflex} \right)\ =\ {{225}^{\circ }}\]
Hence, angle ADC (reflex) inside the quadrilateral is \[{{225}^{\circ }}\].
Now, as we know that angle formed around a point is \[{{360}^{\circ }}\], as we need to rotate \[{{360}^{\circ }}\]. Hence, the sum of angles ADC (reflex) and ADC (outer of quadrilateral) is \[{{360}^{\circ }}\]. And we need to calculate \[\angle ADC\] (outer) from the problem.
So, we can write equation as
\[\angle ADC\ \left( \text{reflex} \right)+\angle ADC\ \left( \text{outer} \right)\ =\ {{360}^{\circ }}\]
\[{{225}^{\circ }}+\angle ADC\ \left( \text{outer} \right)\ =\ {{360}^{\circ }}\]
\[\angle ADC\ \left( \text{outer} \right)\ =\ {{360}^{\circ }}-{{225}^{\circ }}\]
\[=\ {{135}^{\circ }}\]
Hence, the value of \[\angle ADC\] lying on the outer side of the quadrilateral is \[{{135}^{\circ }}\].

Note: Observing ABCD as a quadrilateral is the key point of the question and take the sum of angles of a quadrilateral as \[{{360}^{\circ }}\] not \[{{180}^{\circ }}\]. Sum of interior angles of n sided polygon is given as
$=\ \left( n-2 \right)\times {{180}^{\circ }}$
Don’t confuse with the reflex angle term used in the solution. It is used to define that angle ADC inside the quadrilateral has higher angle than \[{{180}^{\circ }}\], as Reflex angle is defined as angles between \[{{180}^{\circ }}\] and \[{{360}^{\circ }}\] are reflex angles.