
Find Angle ANB = Angle AOB = Angle AMB=?
Answer
425.7k+ views
Hint: In order to solve the given question , we will be using the theorem which states that the angle subtended by an arc at the center is double the angle subtended by it on any point on the remaining part of the circle .
Complete step-by-step answer:
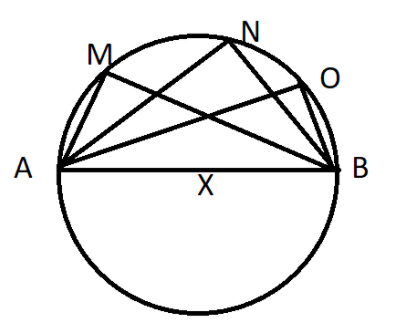
Let us consider the angle ANB first , we can see in the image , AB is the diameter .
Therefore, the angle subtended by the arc AB at the centre is
So,
Similarly , it can be said that angle inscribed in a semicircle is a right angle so Angle ANB = Angle AOB = Angle AMB=
So, the correct answer is “
Note: An arc of a circle is any portion of the circumference of a circle. To recall, the circumference of a circle is the perimeter or distance around a circle. Therefore, we can say that the circumference of a circle is the full arc of the circle itself.
Complete step-by-step answer:

Let us consider the angle ANB first , we can see in the image , AB is the diameter .
Therefore, the angle subtended by the arc AB at the centre is
So,
Similarly , it can be said that angle inscribed in a semicircle is a right angle so Angle ANB = Angle AOB = Angle AMB=
So, the correct answer is “
Note: An arc of a circle is any portion of the circumference of a circle. To recall, the circumference of a circle is the perimeter or distance around a circle. Therefore, we can say that the circumference of a circle is the full arc of the circle itself.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Given that HCF 306 657 9 find the LCM 306 657 class 9 maths CBSE

The highest mountain peak in India is A Kanchenjunga class 9 social science CBSE

What is the difference between Atleast and Atmost in class 9 maths CBSE

What was the capital of the king Kharavela of Kalinga class 9 social science CBSE





