Question

Find by integration the area bounded by the curve ${{y}^{2}}=4ax$ and the lines y = 2a and x=0.

Answer 1

Hint: Plot the curve on the graph paper. Identify the region whose area is to be found. Argue that the area of the region is equal to the difference between the area bounded by the curve y=2a, the x-axis and the ordinates x= 0 and x= a and the area bounded by the curve $y=2\sqrt{a}\sqrt{x}$, the x-axis and the ordinates x=0 and x=a. Use the fact that the area bounded by the curve y=f(x), the x-axis and the ordinates x=a and x= b is given by $A=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$. Hence determine the individual areas and hence the total area.

Complete step-by-step answer:

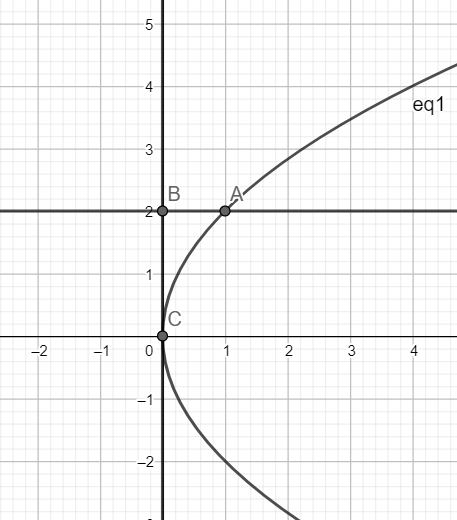
The region whose area is to be found is ABCA.
Finding the coordinates of point A:
We have A is the point of intersection of y = 2a and ${{y}^{2}}=4ax$
Hence, we have $4x=2{{a}^{2}}=4{{a}^{2}}\Rightarrow x=a$
Hence, we have $A\equiv \left( a,2a \right)$
The arm AC of the parabola ${{y}^{2}}=4ax$ has $y\ge 0$
Hence for the arm AC of the parabola, the equation is $y=2\sqrt{a}\sqrt{x}$
As is evident from the graph, the area of the region to be found is the difference between the area bounded by the curve y=2a, the x-axis and the ordinates x= 0 and x= a and the area bounded by the curve $y=2\sqrt{a}\sqrt{x}$, the x-axis and the ordinates x=0 and x=1.
Now, we know that the area of the region bounded by the curve y=f(x), the x-axis and the ordinates x=a and x= b is given by $A=\int_{a}^{b}{\left| f\left( x \right) \right|dx}$.
Hence the area of the region bounded by the curve y = 2a, the x-axis and the ordinates x=0 and x=a is given by ${{A}_{1}}=\int_{0}^{a}{2adx}=2{{a}^{2}}$
Also, the area of the region bounded by the curve $y=2\sqrt{a}\sqrt{x}$, the x-axis and the ordinates x= 0 and x= a is given by ${{A}_{2}}=\int_{0}^{a}{2\sqrt{a}\sqrt{x}dx}=$
We know that $\int{{{x}^{n}}dx}=\dfrac{{{x}^{n+1}}}{n+1}+C$
Hence, we have
${{A}_{2}}=2\sqrt{a}\left( \left. \dfrac{2}{3}{{x}^{\dfrac{3}{2}}} \right|_{0}^{a} \right)=\dfrac{4{{a}^{2}}}{3}$
Hence the required area is given by $A={{A}_{1}}-{{A}_{2}}=2{{a}^{2}}-\dfrac{4{{a}^{2}}}{3}=\dfrac{2{{a}^{2}}}{3}$
Hence the required area is $\dfrac{2{{a}^{2}}}{3}$ square units.

Note: We can also take horizontal strips to find the area as shown below

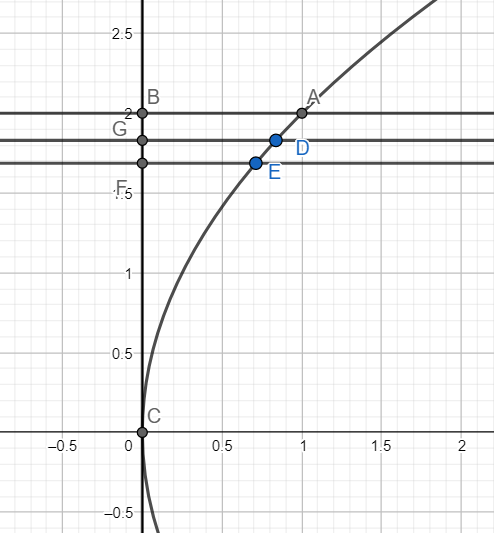
For the strip DEFG, we have GD $=x=\dfrac{{{y}^{2}}}{4a}$ and GF = dy
Hence the area of the region $=\int_{0}^{2a}{\dfrac{{{y}^{2}}}{4a}dy}=\left. \dfrac{{{y}^{3}}}{12a} \right|_{0}^{2a}=\dfrac{2{{a}^{2}}}{3}$, which is the same as obtained above.