Question

Find coordinates of the center of mass of a quarter ring of radius placed in the first quadrant of a Cartesian coordinate system, with center at the origin.

Answer 1

Hint: Quarter ring indicates that we need to find the center of mass for one-fourth of the ring placed in the first quadrant. We will find the general expression of coordinates of a small part of the ring. Finally, we will integrate it to find the required coordinates using the basic formula.

Formula Used:
${{X}_{CM}}=\dfrac{1}{M}\int{xdm}$
${{Y}_{CM}}=\dfrac{1}{M}\int{ydm}$

Complete step-by-step solution:
Here, we need to find the coordinates of the centre of mass of one fourth of a ring placed in the first quadrant. We will assume the origin as the centre of the circle, of which the ring is a part of, and then we can draw the diagram as follows:

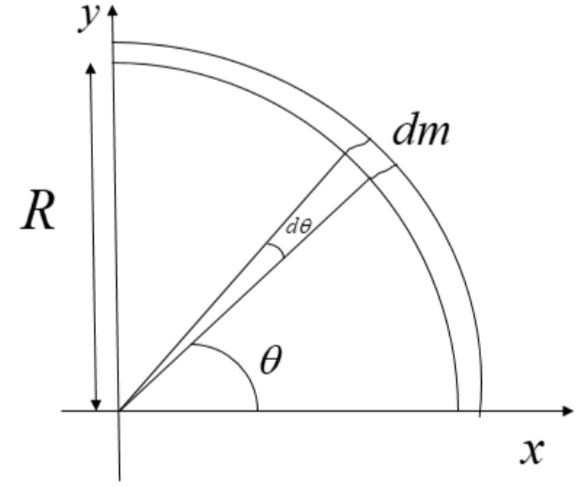
Here, consider a one fourth ring present in the first quadrant having a total mass $M$ and radius $R$ and subtending a total angle of $\dfrac{\pi }{2}$ at the origin.
To find the centre of mass, consider a small portion of the ring at an angle $\theta $ from the x-axis. Let the mass of this portion be $dm$ of length $l$ and the angle subtended by this portion at the origin be $d\theta $.
Here, we will find the $x$ as well as $y$ component of the centre of mass and hence the coordinates of centre of mass.
Here, the total mass $M$ subtends an angle of $\dfrac{\pi }{2}$. Also, the mass $dm$ subtends an angle of $d\theta $
Hence, the mass $dm$can be written as:
$dm=\dfrac{M}{\left( \pi /2 \right)}\times d\theta $ ----(i)
Also, the length of the mass $dm$ can be written as:
$d\theta =\dfrac{l}{R}$
$\Rightarrow l=Rd\theta $ ----(ii)
Also, at any angle $\theta $ the general x coordinate and y coordinate can be written as:
$x=R\cos \theta $
$y=R\sin \theta $
For x coordinate:
${{X}_{CM}}=\dfrac{1}{M}\int{xdm}$
$\Rightarrow {{X}_{CM}}=\dfrac{1}{M}\int{R\cos \theta dm}$
From equation (i)
$\Rightarrow {{X}_{CM}}=\dfrac{1}{M}\int{R\cos \theta \dfrac{M}{(\pi /2)}\times d\theta }$
$\Rightarrow {{X}_{CM}}=\dfrac{2R}{\pi }\int\limits_{0}^{\pi /2}{\cos \theta d\theta }$
$\Rightarrow {{X}_{CM}}=\dfrac{2R}{\pi }$
For y coordinate:
${{Y}_{CM}}=\dfrac{1}{M}\int{ydm}$
$\Rightarrow {{Y}_{CM}}=\dfrac{1}{M}\int{R\sin \theta dm}$
From equation (i)
${{Y}_{CM}}=\dfrac{1}{M}\int{R\sin \theta \dfrac{M}{(\pi /2)}d\theta }$
$\Rightarrow {{Y}_{CM}}=\dfrac{2R}{\pi }\int\limits_{0}^{\pi /2}{\sin \theta d\theta }$
$\Rightarrow {{Y}_{CM}}=\dfrac{2R}{\pi }$
Hence, the coordinates of the centre of mass of a quarter ring placed in the first quadrant is $({{X}_{CM}},{{Y}_{CM}})=(\dfrac{2R}{\pi },\dfrac{2R}{\pi })$.

Note: To find centre of mass, always take a small mass into consideration. Find out the general equation for the x and y coordinate for that small part. Then use the basic formula to find the coordinates of the centre of mass.