Question

How do you find experimentally the refractive index of material of a prism?

Answer 1

Hint : We need to construct a table with various values of angle of incidence of light falling on a prism and angle of deviation determined. Then the refractive index formula using angle of prism and deviation is used to find the refractive index of the material of the prism.

Formula Used: The formulae used in the solution are given here.
 $\Rightarrow \eta {\text{ }} = {\raise0.7ex\hbox{ $ {\sin \left[ {\dfrac{{\left( {A + D} \right)}}{2}} \right]} $ } \!\mathord{\left/
 {\vphantom {{\sin \left[ {\dfrac{{\left( {A + D} \right)}}{2}} \right]} {\sin \dfrac{A}{2}}}}\right.}
\!\lower0.7ex\hbox{ $ {\sin \dfrac{A}{2}} $ }} $ where $ \eta $ is the refractive index of the prism, $ A $ is the angle of prism and $ d $ is the deviation.

Complete step by step answer

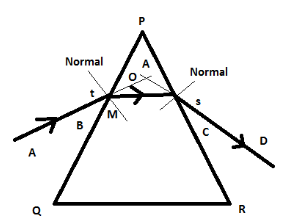
The experiment can be explained as below,
Aim: Finding the refractive index of the prism.
Material required: Prism, piece of white chart paper, pencil, pins, scale and protractor.
Procedure:
1. A prism is placed on the white chart with the triangular base on the chart. The base is traced before removing the prism.
2. The vertices of this triangle are named P, Q and R, as shown in the figure. The angle of the prism, $ \angle QPR = A $ .
3. At a point M on the side PQ, a line is drawn perpendicular to PQ.
4. At M, along the normal an angle of $ 30^\circ $ is marked. A line is then drawn up to M. This is the angle of incidence and its measure is noted.
5. The prism in its position again and two pins are fixed vertically on the line at point A and B.
6. The images of pins through the prism from the other side are found and two other pins are fixed at points C and D in such a way that all the four pins appear to lie along the same straight line.
7. The prism is removed. A line joining the two pin-holes formed by the pins to meet surface PR.
8. The angle between the normal at N and the emergent ray is the angle of emergence.
9. M and N are joined. A, B, M, N, C, D represents the path of light.
10. Both the incident and emergent rays meet at a point ‘O’. The angle between these two rays is the angle of deviation.
11. The same process is repeated for various angles of incidence such as $ 40^\circ $ , $ 50^\circ $ etc.
12. Taking angle of incidence along $ x $ -axis and the angle of deviation along $ y $ -axis we get the graph as shown in figure.
13. The refractive index of prism is given by the formula,
 $\Rightarrow \eta {\text{ }} = {\raise0.7ex\hbox{ $ {\sin \left[ {\dfrac{{\left( {A + D} \right)}}{2}} \right]} $ } \!\mathord{\left/
 {\vphantom {{\sin \left[ {\dfrac{{\left( {A + D} \right)}}{2}} \right]} {\sin \dfrac{A}{2}}}}\right.}
\!\lower0.7ex\hbox{ $ {\sin \dfrac{A}{2}} $ }} $ where $ \eta $ is the refractive index of the prism, $ A $ is the angle of prism and $ d $ is the deviation.
Using this formula, the refractive index of the material of the prism can be measured.

Note
A spectrometer can also be used to find the refractive index of a prism. It uses Snell’s law to find the refractive index. Prism is used to get a spectrum of light. Refraction takes place in prism.