Question

Find out how many AU are there in a parsec.

Answer 1

Hint: In this question we need to convert parsec into AU. Both parsec and AU (astronomical unit) are units of length and are used to measure large distances e.g. distances between stars and planets are measured in these units. For this conversion we will use the simple unitary method.

Formula used:
$\tan \theta = \dfrac{{perpendicular}}{{base}}$
$1\operatorname{arcsec} = {(\dfrac{1}{{3600}})^o} \times \dfrac{\pi }{{{{180}^o}}}$

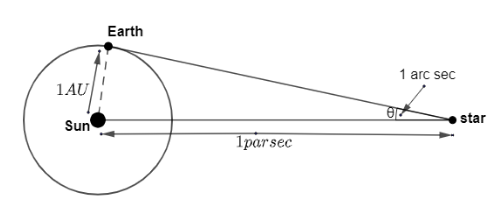
Complete step by step answer:
Parsec is defined as the distance at which the radius of orbit of Earth subtends a parallax angle of one arc second and one arc second is $\dfrac{1}{{3600}}$ of a degree.We will convert the degree to radians as ${1^o} = \dfrac{\pi }{{{{180}^o}}}$.An Astronomical Unit (AU) is defined as the distance of Earth from the Sun. However, the actual distance between the Earth and the Sun varies when Earth goes from aphelion to perihelion. Because of this variation, the Astronomical Unit is defined to be equal to \[149,597,870,700\;\] m.

Now, from the diagram, we can say that $\tan \theta = \dfrac{{1AU}}{{1par\sec }}$.As the distance between the Sun and star is very large as compared to the distance between the Sun and the Earth. So, we can approximate $\tan \theta \simeq \theta $ and $\theta $ here is equal to one arc second.
$1\operatorname{arcsec} = \dfrac{{1AU}}{{1par\sec }}$
$\Rightarrow {(\dfrac{1}{{3600}})^o} \times \dfrac{\pi }{{{{180}^o}}} = \dfrac{{1AU}}{{1par\sec }} \\
\therefore 1par\sec = \dfrac{{648,000}}{\pi }AU \\ $
Hence, one parsec corresponds to $\dfrac{{648,000}}{\pi }$ astronomical units.

Note: The word Parsec is derived from the words ‘parallax’ and ‘arc second’. The astronomical unit is mainly used to assess distances within the Solar System or between stars whereas parsec is used to quantify distances beyond the solar system. In light years, parsec is nearly equal to \[3.26\] light years and astronomical units are approximately equal to $8$ light minutes.