Answer
Verified456.6k+ views
Hint: We first find the relation between the diagonal length of the cylinder to the radius of the circle. This equation will help to build the function of the volume of the cylinder to find its maximum value possible. We then apply the theorem of maxima and minima to find the possible value of the altitude. We have to apply the differentiation in that case.
Complete step-by-step solution:
We know the volume of a cylinder is $\pi {{r}^{2}}h$ cubic unit where r is the radius of the figure and “h” is the height.
Now we need to fit a cylinder of the greatest possible volume in a sphere of radius $R=3\sqrt{3}$ then the relation between those two figures will be ${{R}^{2}}={{r}^{2}}+{{\left( \dfrac{h}{2} \right)}^{2}}$ as the part ${{r}^{2}}+{{\left( \dfrac{h}{2} \right)}^{2}}$ represents the diagonal length of the cylinder which is also the radius of the circle.
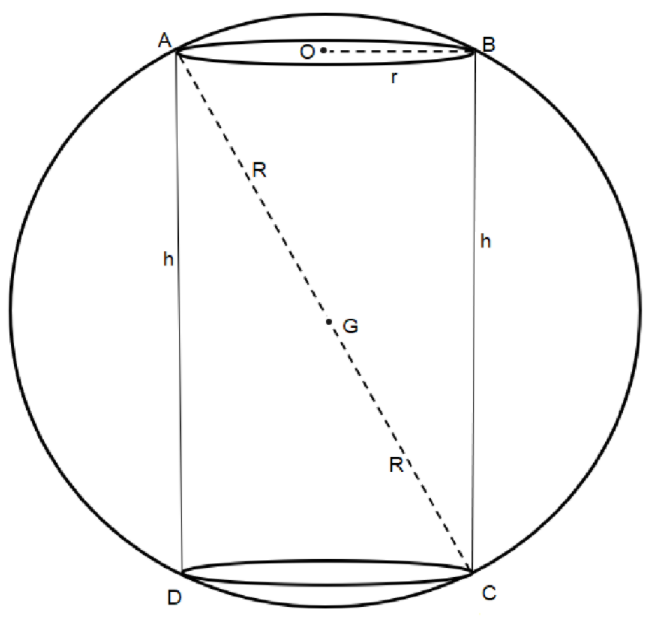
Putting the value, we get ${{\left( 3\sqrt{3} \right)}^{2}}={{r}^{2}}+{{\left( \dfrac{h}{2} \right)}^{2}}\Rightarrow {{r}^{2}}+\dfrac{{{h}^{2}}}{4}=27$ …(i)
Let’s take the volume of a cylinder as a function $v=\pi {{r}^{2}}h$ …(ii)
We replace value of r from equation (i) into equation (ii) to get $v=\pi {{r}^{2}}h=\pi \left( 27-\dfrac{{{h}^{2}}}{4} \right)h$.
Now we apply the theorem of maxima and minima as we need the greatest possible volume v.
So, we differentiae v with respect to h to get \[\dfrac{dv}{dh}=\dfrac{d}{dh}\left[ \pi \left( 27-\dfrac{{{h}^{2}}}{4} \right)h \right]=27\pi -\dfrac{3\pi {{h}^{2}}}{4}\].
We take $\dfrac{dv}{dh}=0$ which gives \[27\pi -\dfrac{3\pi {{h}^{2}}}{4}=0\Rightarrow \dfrac{3\pi {{h}^{2}}}{4}=27\pi \].
We solve it to get the value of h as \[{{h}^{2}}=36\Rightarrow h=\pm 6\].
Now to find the value of $\dfrac{{{d}^{2}}v}{d{{h}^{2}}}$ which is \[\dfrac{{{d}^{2}}v}{d{{h}^{2}}}=\dfrac{d}{dh}\left( \dfrac{dv}{dh} \right)=\dfrac{d}{dh}\left( 27\pi -\dfrac{3\pi {{h}^{2}}}{4} \right)=-\dfrac{3\pi h}{2}\].
We put value of h in $\dfrac{{{d}^{2}}v}{d{{h}^{2}}}$ to get the negative value. As at the point where the second derivative of the function hits a negative value, the main function hits the maximum value.
For h = 6, \[\dfrac{{{d}^{2}}v}{d{{h}^{2}}}=-\dfrac{3\pi h}{2}=-9\pi <0\] which means value of v will be maximum.
For h = -6, \[\dfrac{{{d}^{2}}v}{d{{h}^{2}}}=-\dfrac{3\pi h}{2}=9\pi >0\] which means value of v will be minimum.
So, we take the value of “h” as 6 which is the altitude of the cylinder.
Note: We need to remember the relation of the cylinder and the circle is created from the right-angle triangle. Without that relation, we can’t get the function of volume. We also have to find the value of $\dfrac{{{d}^{2}}v}{d{{h}^{2}}}$ as that helps in finding the maximum value.
Complete step-by-step solution:
We know the volume of a cylinder is $\pi {{r}^{2}}h$ cubic unit where r is the radius of the figure and “h” is the height.
Now we need to fit a cylinder of the greatest possible volume in a sphere of radius $R=3\sqrt{3}$ then the relation between those two figures will be ${{R}^{2}}={{r}^{2}}+{{\left( \dfrac{h}{2} \right)}^{2}}$ as the part ${{r}^{2}}+{{\left( \dfrac{h}{2} \right)}^{2}}$ represents the diagonal length of the cylinder which is also the radius of the circle.
Putting the value, we get ${{\left( 3\sqrt{3} \right)}^{2}}={{r}^{2}}+{{\left( \dfrac{h}{2} \right)}^{2}}\Rightarrow {{r}^{2}}+\dfrac{{{h}^{2}}}{4}=27$ …(i)
Let’s take the volume of a cylinder as a function $v=\pi {{r}^{2}}h$ …(ii)
We replace value of r from equation (i) into equation (ii) to get $v=\pi {{r}^{2}}h=\pi \left( 27-\dfrac{{{h}^{2}}}{4} \right)h$.
Now we apply the theorem of maxima and minima as we need the greatest possible volume v.
So, we differentiae v with respect to h to get \[\dfrac{dv}{dh}=\dfrac{d}{dh}\left[ \pi \left( 27-\dfrac{{{h}^{2}}}{4} \right)h \right]=27\pi -\dfrac{3\pi {{h}^{2}}}{4}\].
We take $\dfrac{dv}{dh}=0$ which gives \[27\pi -\dfrac{3\pi {{h}^{2}}}{4}=0\Rightarrow \dfrac{3\pi {{h}^{2}}}{4}=27\pi \].
We solve it to get the value of h as \[{{h}^{2}}=36\Rightarrow h=\pm 6\].
Now to find the value of $\dfrac{{{d}^{2}}v}{d{{h}^{2}}}$ which is \[\dfrac{{{d}^{2}}v}{d{{h}^{2}}}=\dfrac{d}{dh}\left( \dfrac{dv}{dh} \right)=\dfrac{d}{dh}\left( 27\pi -\dfrac{3\pi {{h}^{2}}}{4} \right)=-\dfrac{3\pi h}{2}\].
We put value of h in $\dfrac{{{d}^{2}}v}{d{{h}^{2}}}$ to get the negative value. As at the point where the second derivative of the function hits a negative value, the main function hits the maximum value.
For h = 6, \[\dfrac{{{d}^{2}}v}{d{{h}^{2}}}=-\dfrac{3\pi h}{2}=-9\pi <0\] which means value of v will be maximum.
For h = -6, \[\dfrac{{{d}^{2}}v}{d{{h}^{2}}}=-\dfrac{3\pi h}{2}=9\pi >0\] which means value of v will be minimum.
So, we take the value of “h” as 6 which is the altitude of the cylinder.
Note: We need to remember the relation of the cylinder and the circle is created from the right-angle triangle. Without that relation, we can’t get the function of volume. We also have to find the value of $\dfrac{{{d}^{2}}v}{d{{h}^{2}}}$ as that helps in finding the maximum value.