Question

Find out the equivalent focal length of the given lens combination.

$\begin{align}
  & (A)\dfrac{R}{{{\mu }_{1}}-{{\mu }_{2}}} \\
 & (B)\dfrac{2R}{{{\mu }_{1}}-{{\mu }_{2}}} \\
 & (C)\dfrac{4R}{{{\mu }_{1}}-{{\mu }_{2}}} \\
 & (D)\dfrac{R}{{{\mu }_{1}}+{{\mu }_{2}}} \\
\end{align}$

Answer 1

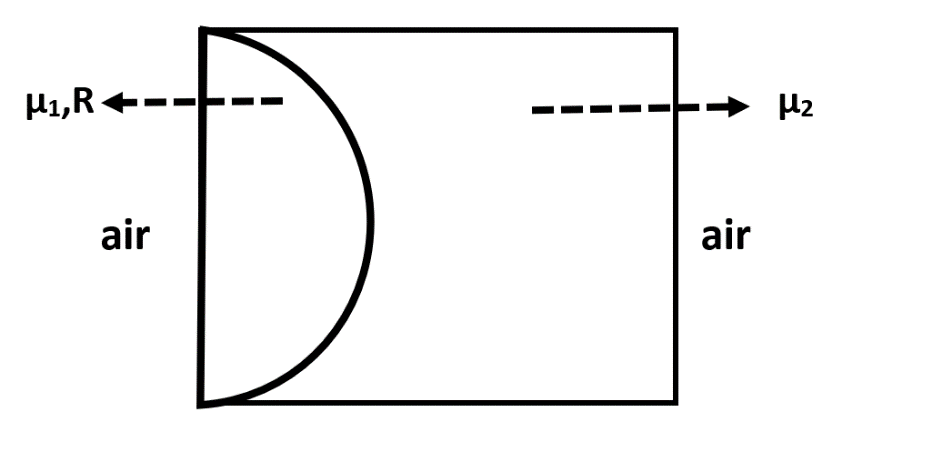
Hint: The combination of lenses in the given figure are plano convex lens and plano concave lens and these lenses have a common surface of contact. Also on the other side of the convex lens we have air and on the other side of the concave lens, we have air. Thus we shall find the focal length of both lenses separately and use the formula of finding the combined focal length of more than one lens set up.

Complete answer:
Since these are lenses with two different focal lengths at each side, therefore we will use Lens maker’s formula to write their respective focal lengths. Mathematically, the lens maker’s formula can be written as:
$\Rightarrow \dfrac{1}{f}=(\mu -1)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]$
Where,
$f$ is the focal length.
$\mu $ is the refractive index of glass used. And,
${{R}_{1}}$ and ${{R}_{2}}$ are the radius of curvature of two sides of the lens.
Now, let the focal length of plano convex lens be given by ${{f}_{1}}$ and let the focal length of plano concave lens be given by ${{f}_{2}}$ . Then, we can calculate them as follows:
$\begin{align}
  & \Rightarrow \dfrac{1}{{{f}_{1}}}=({{\mu }_{1}}-1)\left[ \dfrac{1}{\infty }-\left( \dfrac{1}{-R} \right) \right] \\
 & \Rightarrow \dfrac{1}{{{f}_{1}}}=\dfrac{({{\mu }_{1}}-1)}{R} \\
\end{align}$
And for second lens, we have:
$\begin{align}
  & \Rightarrow \dfrac{1}{{{f}_{2}}}=({{\mu }_{2}}-1)\left[ \left( \dfrac{1}{-R} \right)-\dfrac{1}{\infty } \right] \\
 & \Rightarrow \dfrac{1}{{{f}_{2}}}=\dfrac{({{\mu }_{2}}-1)}{-R} \\
\end{align}$
Now, for a combination of lens having different focal lengths, the resultant focal length (say ${{f}_{R}}$) can be written as:
$\Rightarrow \dfrac{1}{{{f}_{R}}}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$
Putting the values of all the respective terms in the above equation, we get:
$\begin{align}
  & \Rightarrow \dfrac{1}{{{f}_{R}}}=\dfrac{({{\mu }_{1}}-1)}{R}+\dfrac{({{\mu }_{2}}-1)}{-R} \\
 & \Rightarrow \dfrac{1}{{{f}_{R}}}=\dfrac{{{\mu }_{1}}-1-{{\mu }_{2}}+1}{R} \\
 & \Rightarrow \dfrac{1}{{{f}_{R}}}=\dfrac{{{\mu }_{1}}-{{\mu }_{2}}}{R} \\
 & \therefore {{f}_{R}}=\dfrac{R}{{{\mu }_{1}}-{{\mu }_{2}}} \\
\end{align}$
Hence, the equivalent focal length of the given lens combination is equal to $\dfrac{R}{{{\mu }_{1}}-{{\mu }_{2}}}$.

Hence, option (A) is the correct option.

Note:
There are many different formulas and theories in the chapter of optics. So, one should know which formula is to be applied when. This lens used in this problem is attached perpendicularly. If they were attached side by side then the resultant lens would be a bifocal lens which is generally used by old people.