Question

Find the altitude of a rhombus whose area is $320c{m^2}$ and side is $5m.$

Answer 1

Hint: According to given in the question we have to determine the altitude of a rhombus whose area is $320c{m^2}$and side is $5m.$So, first of all we have to know about which is as explained below:
Rhombus: Rhombus where its four sides are equal but four angles are not equal to ${90^0}$but its diagonals intersect each other at ${90^0}$.
Now, we have to understand about the altitude of the rhombus which is as explained below:
Altitude of the rhombus: Altitude of the rhombus is a perpendicular distance from the base to the opposite side.
Now, to determine the altitude for the given rhombus we just have to use the formula to determine the altitude which is as mentioned below:

Formula used:
$ \Rightarrow $Altitude of rhombus$ = \dfrac{A}{b}.................(1)$
Where, A is the area and b is the side of the rhombus.
Now, on substituting all the values in the formula (A) as mentioned above we can determine the length of altitude.

Complete step by step answer:
Step 1: First of all as mentioned in the solution hint that Rhombus where its four sides are equal but four angles are not equal to ${90^0}$ but its diagonals intersect each other at ${90^0}$.
Step 2: Now, to find the altitude as we know that altitude of the rhombus is a perpendicular distance from the base to the opposite side. Which is AE and the side of the rhombus is AD = DC = 5cm.

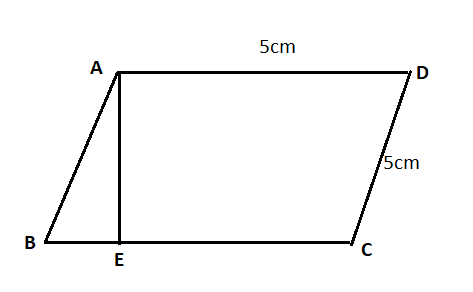
Step 3: Now, to find the altitude which is AE we have to use the formula (1) as mentioned in the solution hint. Hence, on substituting all the values in the formula (A),
$
   \Rightarrow AE = \dfrac{{320}}{5} \\
   \Rightarrow AE = 64cm \\
 $

Hence, with the help of the formula (A) as mentioned in the solution hint we have determined the altitude of the rhombus ABCD which is $AE = 64cm$.

Note: Rhombus has its four sides are equal but four angles are not equal to ${90^0}$ but its diagonals intersect each other at ${90^0}$.
The altitude of the rhombus is a perpendicular distance from the base to the opposite side.